| Codeforces Round 847 (Div. 3) |
|---|
| Закончено |
Тимофей приехал в известную летнюю школу и нашел там дерево на $$$n$$$ вершинах. Дерево — это связный неориентированный граф без циклов.
Каждая вершина этого дерева, кроме $$$c_0$$$, покрашена в белый цвет. Вершина $$$c_0$$$ покрашена в черный цвет.
Тимофей хочет покрасить все вершины этого дерева в черный цвет. Для этого он выполняет $$$n - 1$$$ операцию. Во время $$$i$$$-й операции он выбирает белую вершину $$$c_i$$$ и красит ее в черный цвет.
Назовем позитивностью дерева минимальное расстояние между всеми парами различных черных вершин в нем. Расстоянием между вершинами $$$v$$$ и $$$u$$$ называется количество ребер на пути от $$$v$$$ до $$$u$$$.
После каждой очередной покраски Тимофей хочет знать позитивность текущего дерева.
В первой строке записано число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
В первой строке каждого набора входных данных записаны числа $$$n, c_0$$$ ($$$2 \le n \le 2 \cdot 10^5$$$, $$$1 \le c_0 \le n$$$) — количество вершин в дереве и номер начальной черной вершины.
Во второй строке каждого набора входных данных записано $$$n - 1$$$ различных чисел $$$c_1, c_2, \dots, c_{n-1}$$$ ($$$1 \le c_i \le n$$$, $$$c_i \ne c_0$$$), где $$$c_i$$$ это вершина, покрашенная в черный цвет во время $$$i$$$-й операции.
В следующей $$$n - 1$$$ строке каждого набора входных данных записаны числа $$$v_i, u_i$$$ ($$$1 \le v_i, u_i \le n$$$) — ребра в дереве.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите в отдельной строке $$$n - 1$$$ число.
Число с номером $$$i$$$ должно быть равно позитивности дерева, полученного первыми $$$i$$$ покрасками.
66 64 1 3 5 22 46 55 33 41 34 24 1 33 12 31 410 310 7 6 5 2 9 8 1 41 21 34 54 36 48 79 810 81 87 37 5 1 2 4 61 23 24 53 46 57 69 79 3 1 4 2 6 8 54 18 94 82 67 32 43 55 410 21 8 5 10 6 9 4 3 710 77 83 69 77 64 21 67 59 2
3 2 1 1 1 3 1 1 3 2 2 2 2 2 1 1 1 4 2 2 1 1 1 5 1 1 1 1 1 1 1 4 3 2 2 1 1 1 1 1
В первом наборе входных данных, после второй покраски, дерево выглядит так: 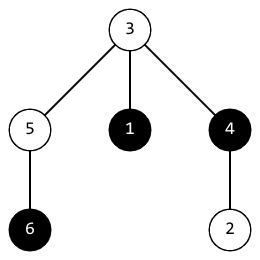
Расстояние между вершинами $$$1$$$ и $$$6$$$ равно $$$3$$$, расстояние между вершинами $$$4$$$ и $$$6$$$ равно $$$3$$$, расстояние между вершинами $$$1$$$ и $$$4$$$ равно $$$2$$$. Позитивность такого дерева равна минимуму из этих расстояний, то есть $$$2$$$.
В третьем наборе входных данных, после четвертой покраски, дерево выглядит так: 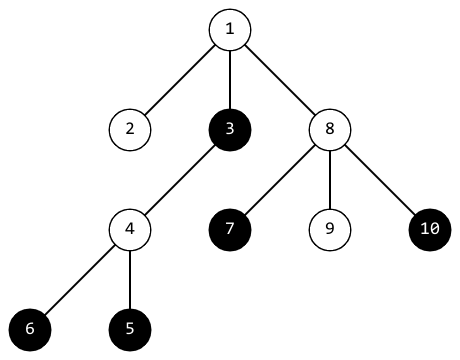
Позитивность такого дерева равна $$$2$$$.
| Название |
|---|




