| VK Cup 2022 - Отборочный раунд (Engine) |
|---|
| Закончено |
В доме Вики есть комната в форме прямоугольного параллелепипеда. Пол комнаты — прямоугольник размером $$$w \times d$$$, а потолок находится над полом на постоянной высоте $$$h$$$. Введем на полу систему координат таким образом, чтобы углы комнаты имели координаты $$$(0, 0)$$$, $$$(w, 0)$$$, $$$(w, d)$$$ и $$$(0, d)$$$.
Ноутбук стоит на полу в точке $$$(a, b)$$$. Проектор висит на потолке прямо над точкой $$$(f, g)$$$. Вика хочет соединить ноутбук и проектор кабелем таким образом, чтобы кабель все время шел вдоль стен, потолка или пола (то есть не висел внутри комнаты). Кроме того, кабель должен всегда идти параллельно одной из сторон параллелепипеда (то есть он не может идти по диагонали).
Какова минимальная длина кабеля необходима, чтобы соединить ноутбук и проектор?
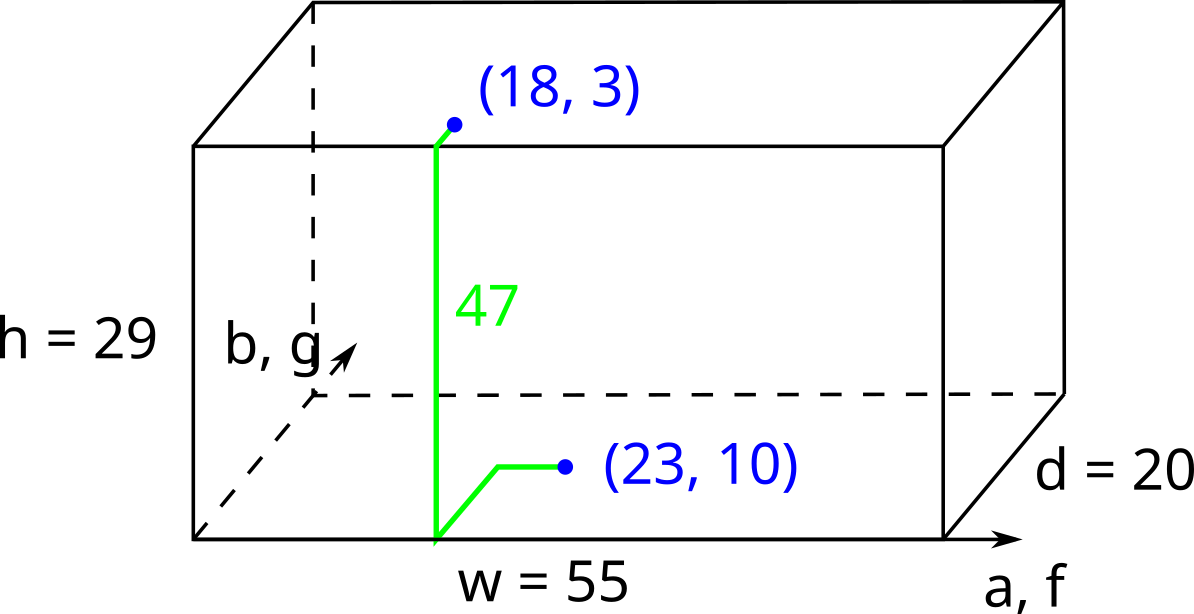 Рисунок для первого набора входных данных. Один из оптимальных способов проложить кабель изображён зеленым цветом.
Рисунок для первого набора входных данных. Один из оптимальных способов проложить кабель изображён зеленым цветом. Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит три целых числа $$$w$$$, $$$d$$$ и $$$h$$$ ($$$2 \le w, d, h \le 1000$$$) — размеры комнаты.
Вторая строка содержит четыре целых числа $$$a$$$, $$$b$$$, $$$f$$$, $$$g$$$ ($$$0 < a, f < w$$$; $$$0 < b, g < d$$$): ноутбук расположен на полу в точке $$$(a, b)$$$, а проектор — на потолке прямо над точкой $$$(f, g)$$$.
Для каждого набора входных данных выведите одно целое число — минимальную длину кабеля, необходимую для того, чтобы соединить ноутбук и проектор, причём так, чтобы кабель все время шел вдоль стен, пола и потолка комнаты, а также всё время шёл параллельно одной из сторон параллелепипеда.
555 20 2923 10 18 320 10 51 5 2 515 15 47 13 10 102 1000 21 1 1 99910 4 107 1 2 1
47 8 14 1002 17
На рисунке в условии задачи изображен первый набор входных данных.
| Название |
|---|




