| Hello 2023 |
|---|
| Закончено |
Время пришло, MKnez и Балтик должны наконец-то провести Игры века. Для этого они построили деревню для размещения всех участников.
Деревня имеет вид равностороннего треугольника, ограниченного тремя дорогами длины $$$n$$$. Она разделена на $$$n^2$$$ меньших равносторонних треугольников со стороной $$$1$$$ с помощью $$$3n-3$$$ дополнительных дорог, параллельных сторонам, см. рисунок для $$$n=3$$$. Каждая из $$$3n$$$ дорог состоит из нескольких (возможно, $$$1$$$) участков дороги длины $$$1$$$, соединяющих соседние перекрестки.
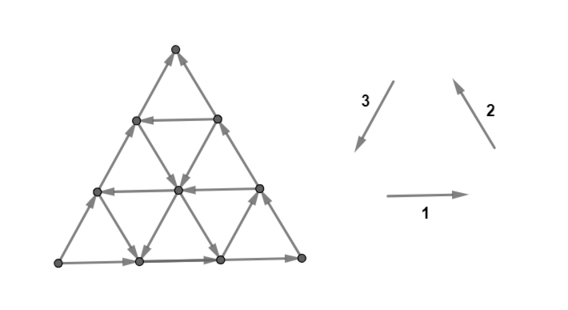
Для всех $$$3n$$$ дороги уже выбраны направления (то есть, для каждой дороги выбрано одно и то же направление для всех ее участков). Транспорт может двигаться по участкам дорог только в выбранном направлении (т. е. дороги односторонние).
Ваша задача — внести поправки в план движения так, чтобы от каждого перекрестка можно было доехать до любого другого. А именно, вы можете изменять направление движения на любом участке дороги длины $$$1$$$. Чему равно минимальное количество участков дорог, на которых нужно изменить направление?
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \leq t \leq 10\,000$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит целое положительное число $$$n$$$ ($$$1\leq n\leq 10^5$$$) — размер стороны треугольной деревни.
Далее следуют три строки, каждая из которых содержит бинарную строку длины $$$n$$$, описывающую направления движения на дорогах.
$$$i$$$-я из этих строк содержит бинарную строку $$$s_i$$$ длины $$$n$$$, описывающую направления на дорогах, параллельных дороге $$$i$$$ на рисунке выше. А именно, $$$j$$$-й символ $$$s_i$$$ равен «1», если $$$j$$$-я кратчайшая дорога (параллельная дороге $$$i$$$ на рисунке) имеет такое же направление, как дорога $$$i$$$ на рисунке, и «0», если ее направление противоположное. Таким образом, первый символ $$$s_i$$$ описывает направление на дороге из $$$1$$$ участка, а последний символ описывает направление на дороге из $$$n$$$ участков.
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$10^5$$$.
Для каждого набора входных данных выведите минимальное количество участков дороги, на которых нужно изменить направление движения.
3300100101010003111011100
2 0 3
Первый пример показан на рисунке в условии. Существует несколько решений, изменяющих направление на ровно $$$2$$$ участках дорог, но изменение направления только на $$$1$$$ участке дороги не может привести к тому, что от каждого перекрестка можно добраться до любого другого. Одно из возможных решений показано на рисунке ниже, измененные участки дорог показаны синим.
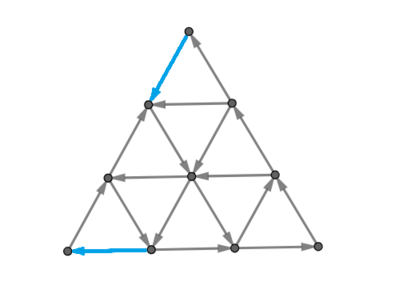
Во втором примере ответ равен $$$0$$$, потому что уже в изначальной конфигурации можно от каждого перекрестка добраться до любого другого.
| Название |
|---|




