| Good Bye 2022: 2023 is NEAR |
|---|
| Закончено |
Косия и Махиру наслаждаются зимним фестивалем. Улицы зимнего фестиваля можно представить как неориентированный граф-сетку размера $$$n \times n$$$. Формально, множество вершин определяется как $$$\{(i,j) \; | \; 1 \leq i,j\leq n \}$$$, и две вершины $$$(i_1,j_1)$$$ и $$$(i_2,j_2)$$$ соединены ребром только тогда когда $$$|i_1-i_2|+|j_1-j_2|=1$$$.
 Граф размера $$$n = 3$$$.
Граф размера $$$n = 3$$$. Косия и Махиру планируют посетить зимний фестиваль, проехав по $$$2n$$$ маршрутам. Сами маршруты еще не определены, но начала и концы маршрутов уже известны:
- На $$$i$$$-м маршруте они начнут из вершины $$$(1, i)$$$ и закончат в вершине $$$(n, p_i)$$$, где $$$p$$$ — перестановка длины $$$n$$$.
- На $$$(i+n)$$$-м маршруте они начнут из вершины $$$(i, 1)$$$ и закончат в вершине $$$(q_i, n)$$$, где $$$q$$$ — перестановка длины $$$n$$$.
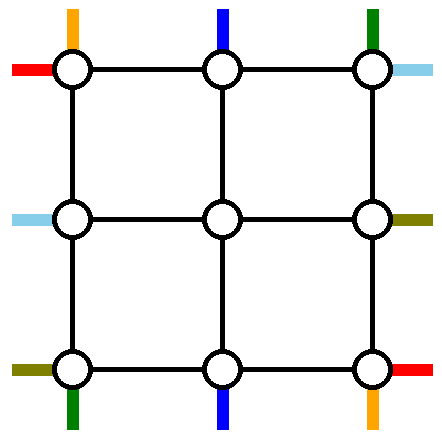 Граф размера $$$n = 3$$$, одинаковыми цветами показаны начала и концы одного маршрута для $$$p = [3, 2, 1]$$$ и $$$q = [3, 1, 2]$$$.
Граф размера $$$n = 3$$$, одинаковыми цветами показаны начала и концы одного маршрута для $$$p = [3, 2, 1]$$$ и $$$q = [3, 1, 2]$$$. Ваша задача — создать схему маршрутов, то есть выбрать $$$2n$$$ путей таких, что каждый путь соединяет заданные начало и конец. Определим загрузку ребра как количество раз, которое это ребро используется (суммарно в обе стороны) в схеме маршрутов. Чтобы Косия и Махиру не слишком скучали от проезда одних и тех же ребер, найдите схему маршрутов, минимизирующую максимальную загрузку среди всех ребер.
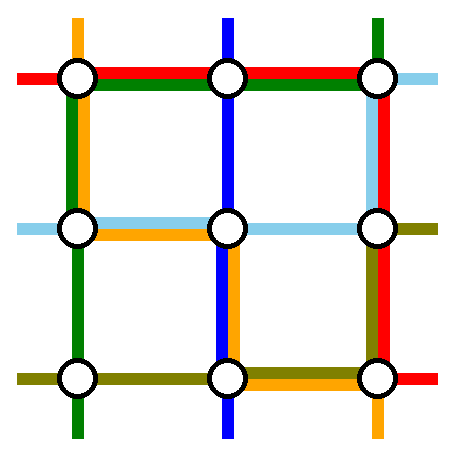 Пример решения. Максимальная загрузка равна $$$2$$$, что оптимально для этого случая.
Пример решения. Максимальная загрузка равна $$$2$$$, что оптимально для этого случая. Первая строка содержит одно целое число $$$n$$$ ($$$2 \leq n \leq 200$$$) — размер сетки графа.
Вторая строка содержит $$$n$$$ целых чисел $$$p_1, p_2, \dots, p_n$$$ ($$$1 \leq p_i \leq n$$$).
Третья строка содержит $$$n$$$ целых чисел $$$q_1, q_2, \dots, q_n$$$ ($$$1 \leq q_i \leq n$$$).
Гарантируется, что и $$$p$$$, и $$$q$$$ являются перестановками длины $$$n$$$.
Выведите $$$2n$$$ строк, каждая из которых описывает маршрут.
Первые $$$n$$$ строк должны описывать маршруты, идущие сверху вниз. $$$i$$$-я строка должна описывать маршрут, начинающийся в вершине $$$(1, i)$$$ и заканчивающийся в вершине $$$(n, p_i)$$$.
Следующие $$$n$$$ строк должны описывать маршруты, идущие слева направо. $$$(i+n)$$$-я строка должна описывать маршрут, начинающийся в вершине $$$(i, 1)$$$ и заканчивающийся в вершине $$$(q_i, n)$$$.
Каждая строка, описывающая маршрут, должна начинаться с числа $$$k$$$ ($$$2 \le k \le 10^5$$$) — количество вершин, через которые проходит маршрут, включая начальную и конечную. Далее выведите все вершины, через которые проходит маршрут, по порядку. Иными словами, если маршрут выглядит как $$$(x_1, y_1) \rightarrow (x_2, y_2) \rightarrow \dots \rightarrow (x_k, y_k)$$$, то выведите $$$k~x_1~y_1~x_2~y_2 \ldots x_k~y_k$$$. Обратите внимание, что $$$|x_i-x_{i+1}|+|y_i-y_{i+1}| = 1$$$ должно выполняться для всех $$$1 \le i < k$$$.
Если существует несколько решений, минимизирующих максимальную загрузку, выведите любое.
3 3 2 1 3 1 2
5 1 1 2 1 2 2 3 2 3 3 3 1 2 2 2 3 2 5 1 3 1 2 1 1 2 1 3 1 5 1 1 1 2 1 3 2 3 3 3 4 2 1 2 2 2 3 1 3 4 3 1 3 2 3 3 2 3
4 3 4 2 1 2 4 1 3
6 1 1 1 2 2 2 2 3 3 3 4 3 6 1 2 1 3 2 3 2 4 3 4 4 4 5 1 3 2 3 2 2 3 2 4 2 7 1 4 1 3 1 2 2 2 2 1 3 1 4 1 7 1 1 2 1 3 1 3 2 3 3 2 3 2 4 6 2 1 2 2 3 2 4 2 4 3 4 4 6 3 1 3 2 3 3 3 4 2 4 1 4 5 4 1 4 2 4 3 3 3 3 4
3 1 2 3 1 2 3
3 1 1 2 1 3 1 3 1 2 2 2 3 2 3 1 3 2 3 3 3 3 1 1 1 2 1 3 3 2 1 2 2 2 3 3 3 1 3 2 3 3
Первый пример соответствует рисункам из условия задачи.
Примеры ответов для примеров $$$2$$$ и $$$3$$$ показаны ниже:
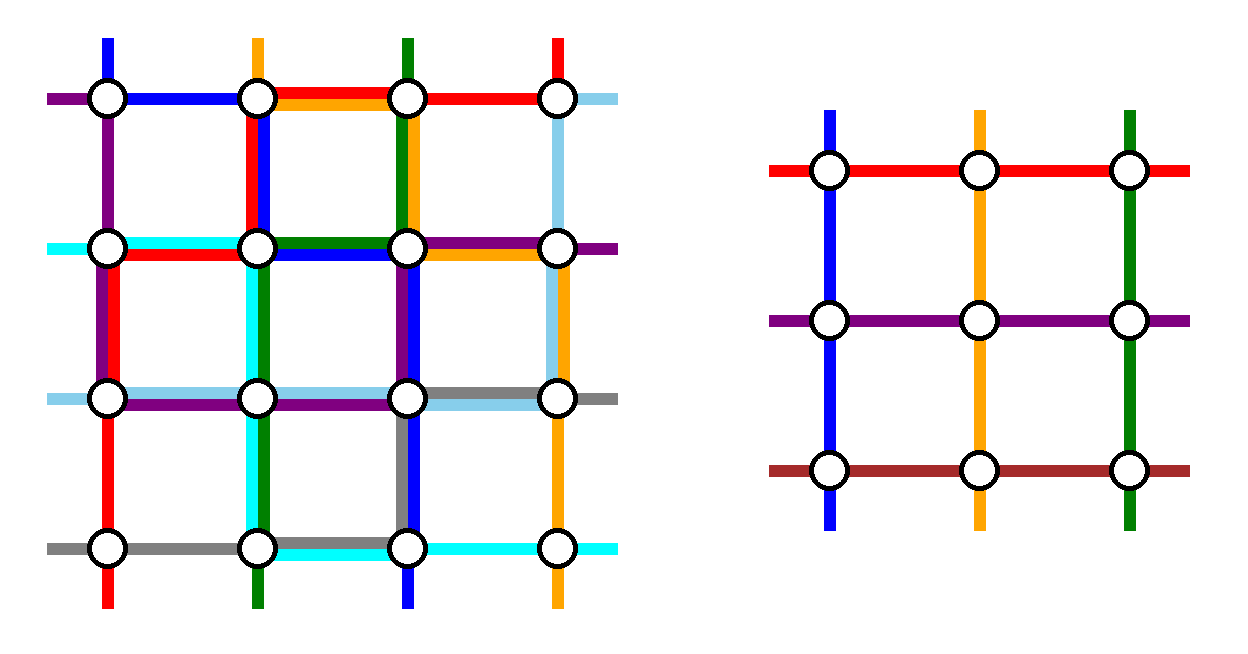 Примеры ответов для примеров $$$2$$$ и $$$3$$$. Максимальная загрузка равна соответственно $$$2$$$ и $$$1$$$.
Примеры ответов для примеров $$$2$$$ и $$$3$$$. Максимальная загрузка равна соответственно $$$2$$$ и $$$1$$$.
| Название |
|---|




