| Good Bye 2022: 2023 is NEAR |
|---|
| Закончено |
У Ими есть неориентированное дерево из $$$n$$$ вершин, ребра которого пронумерованы от $$$1$$$ до $$$n-1$$$. $$$i$$$-е ребро соединят вершины $$$u_i$$$ и $$$v_i$$$. Также на дереве находятся $$$k$$$ бабочек. Изначально $$$i$$$-я бабочка находится в вершине $$$a_i$$$. Все значения $$$a$$$ попарно различны.
Косия играет в игру следующим образом.
- Для $$$i = 1, 2, \dots, n - 1$$$ Косия выбирает одно из направлений $$$i$$$-го ребра ($$$u_i \rightarrow v_i$$$ или $$$v_i \rightarrow u_i$$$) с одинаковой вероятностью.
- Для $$$i = 1, 2, \dots, n - 1$$$, если в начальной вершине $$$i$$$-го ребра есть бабочка, а в конечной вершине нет бабочки, то эта бабочка перелетает в конечную вершину. Обратите внимание, что операции выполняются для ребер $$$1, 2, \dots, n - 1$$$ по порядку, а не одновременно.
- Косия выбирает две бабочки из $$$k$$$ бабочек с равной вероятностью для всех $$$\frac{k(k-1)}{2}$$$ способов выбрать две бабочки, затем она вычисляет расстояние$$$^\dagger$$$ между двумя вершинами, и объявляет это своим счетом.
Косия хочет, чтобы вы вычислили математическое ожидание ее счета по модулю $$$998\,244\,353^\ddagger$$$.
$$$^\dagger$$$ Расстоянием между двумя вершинами в дереве называется количество ребер на (единственном) простом пути между ними.
$$$^\ddagger$$$ Формально, пусть $$$M = 998\,244\,353$$$. Можно показать, что ответ может быть представлен в виде несократимой дроби $$$\frac{p}{q}$$$, где $$$p$$$ и $$$q$$$ — целые числа, и $$$q \not \equiv 0 \pmod{M}$$$. Выведите целое число, равное $$$p \cdot q^{-1} \bmod M$$$. Другими словами, выведите такое целое число $$$x$$$, что $$$0 \le x < M$$$ и $$$x \cdot q \equiv p \pmod{M}$$$.
Первая строка содержит два целых числа $$$n$$$ и $$$k$$$ ($$$2 \leq k \leq n \leq 3 \cdot {10}^5$$$) — размер дерева и количество бабочек.
Вторая строка содержит $$$k$$$ целых чисел $$$a_1, a_2, \dots, a_k$$$ ($$$1 \leq a_i \leq n$$$) — начальные позиции бабочек. Гарантируется, что все позиции попарно различны.
$$$i$$$-я из следующих $$$n − 1$$$ строк содержит два целых числа $$$u_i$$$, $$$v_i$$$ ($$$1 \leq u_i, v_i \leq n$$$, $$$u_i \neq v_i$$$) — вершины, которые соединяет $$$i$$$-е ребро.
Гарантируется, что заданные ребра образуют дерево.
Выведите одно целое число — математическое ожидание счета Косии по модулю $$$998\,244\,353$$$.
3 2 1 3 1 2 2 3
748683266
5 3 3 4 5 1 2 1 3 2 4 2 5
831870296
Дерево из первого примера показано ниже. Вершины с бабочками отмечены жирным.
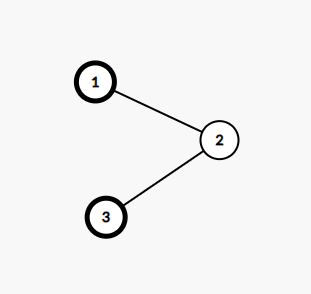
Существуют только $$$2$$$ бабочки, поэтому выбор бабочек фиксирован. Рассмотрим следующие $$$4$$$ случая:
- Ориентация ребер $$$1 \rightarrow 2$$$ и $$$2 \rightarrow 3$$$: бабочка из вершины $$$1$$$ перемещается в вершину $$$2$$$, а бабочка в вершине $$$3$$$ не двигается. Расстояние между вершинами $$$2$$$ и $$$3$$$ равно $$$1$$$.
- Ориентация ребер $$$1 \rightarrow 2$$$ и $$$3 \rightarrow 2$$$: бабочка из вершины $$$1$$$ перемещается в вершину $$$2$$$, а бабочка в вершине $$$3$$$ не двигается, потому что вершина $$$2$$$ занята. Расстояние между вершинами $$$2$$$ и $$$3$$$ равно $$$1$$$.
- Ориентация ребер $$$2 \rightarrow 1$$$ и $$$2 \rightarrow 3$$$: бабочки в вершинах $$$1$$$ и $$$3$$$ не двигаются. Расстояние между вершинами $$$1$$$ и $$$3$$$ равно $$$2$$$.
- Ориентация ребер $$$2 \rightarrow 1$$$ и $$$3 \rightarrow 2$$$: бабочка в вершине $$$1$$$ не двигается, а бабочка из вершины $$$3$$$ перемещается в вершину $$$2$$$. Расстояние между вершинами $$$1$$$ и $$$2$$$ равно $$$1$$$.
Таким образом, математическое ожидание счета Косии равно $$$\frac {1+1+2+1} {4} = \frac {5} {4}$$$, что есть $$$748\,683\,266$$$ по модулю $$$998\,244\,353$$$.
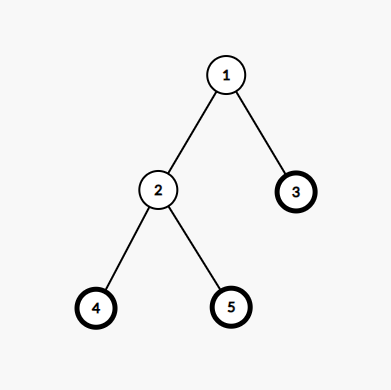
Дерево из второго примера показано ниже. Вершины с бабочками отмечены жирным. Математическое ожидание счета Косии равно $$$\frac {11} {6}$$$, что есть $$$831\,870\,296$$$ по модулю $$$998\,244\,353$$$.
| Название |
|---|




