| ABBYY Cup 2.0 - Easy |
|---|
| Закончено |
В честь проведения второго турнира ABBYY Cup Умный Бобер решил устроить вечеринку. У Бобра много знакомых, и некоторые из них дружат друг с другом, а некоторые друг другу не нравятся. Чтобы вечеринка удалась на славу, Умный Бобер хочет пригласить только тех своих знакомых, которые дружат, и не приглашать тех, кто не нравится друг другу. Отношения дружбы и антипатии симметричны.
Более формально, для каждого приглашенного человека должны выполняться следующие условия:
- все его друзья должны быть также приглашены на вечеринку;
- среди приглашенных не должно быть людей, которые ему не нравятся;
- все приглашенные на вечеринку должны быть связаны с ним дружбой напрямую или через цепь общих друзей произвольной длины. Будем говорить, что люди a1 и ap связаны цепью общих друзей, если существует последовательность людей a2, a3, ..., ap - 1 такая, что все пары людей ai и ai + 1 (1 ≤ i < p) — друзья.
Помогите Бобру определить максимальное количество знакомых, которых он сможет пригласить.
В первой строке входных данных записано целое число n — количество знакомых Бобра.
Во второй строке записано целое число k 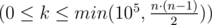 — количество пар друзей. В следующих k строках через пробел записаны пары чисел ui, vi
— количество пар друзей. В следующих k строках через пробел записаны пары чисел ui, vi 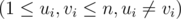 — номера людей, которые входят в i-ую пару друзей.
— номера людей, которые входят в i-ую пару друзей.
В следующей строке записано число m 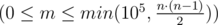 — количество пар людей, которые друг другу не нравятся. В следующих m строках перечислены пары таких людей в том же формате, что и пары друзей.
— количество пар людей, которые друг другу не нравятся. В следующих m строках перечислены пары таких людей в том же формате, что и пары друзей.
Каждая пара людей упоминается во входных данных не более одного раза 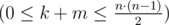 . В частности, два человека не могут быть друзьями и одновременно не нравиться друг другу.
. В частности, два человека не могут быть друзьями и одновременно не нравиться друг другу.
Ограничения на входные данные для получения 30 баллов:
- 2 ≤ n ≤ 14
Ограничения на входные данные для получения 100 баллов:
- 2 ≤ n ≤ 2000
Выведите единственное число — максимальное количество людей, которых Бобер сможет пригласить на вечеринку. Если группу людей, удовлетворяющую всем требованиям, выбрать невозможно, выведите 0.
9
8
1 2
1 3
2 3
4 5
6 7
7 8
8 9
9 6
2
1 6
7 9
3
Рассмотрим пример.
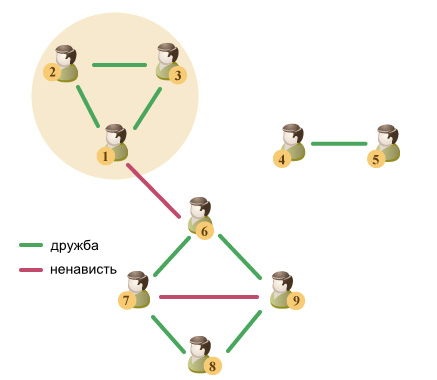
Под условия задачи подходят две группы людей: {1, 2, 3} и {4, 5}, при этом ответом будет размер наибольшей из этих групп. Группа {6, 7, 8, 9} не подходит, так как в ней есть люди 7 и 9, которые не нравятся друг другу. Группа {1, 2, 3, 4, 5} также не подходит, так как не все ее члены связаны цепью общих друзей (например, люди 2 и 5 не связаны).
| Название |
|---|




