| Codeforces Global Round 24 |
|---|
| Закончено |
У Дореми есть реберно-взвешенное дерево из $$$n$$$ вершин, веса являются целыми числами от $$$1$$$ до $$$10^9$$$. Дореми провела $$$\frac{n(n+1)}{2}$$$ экспериментов с деревом.
В каждом эксперименте Дореми выбирает две вершины $$$i$$$ и $$$j$$$ такие, что $$$j \leq i$$$, и соединяет их дополнительным ребром веса $$$1$$$. После этого в графе образовывается один цикл (или петля, если $$$i=j$$$). Дореми определяет $$$f(i,j)$$$ как сумму длин кратчайших путей от каждой вершины до цикла.
Формально, пусть $$$\mathrm{dis}_{i,j}(x,y)$$$ — длина кратчайшего пути между вершинами $$$x$$$ и $$$y$$$, когда в дерево добавлено одно ребро $$$(i,j)$$$ веса $$$1$$$, а $$$S_{i,j}$$$ — множество вершин на цикле, когда добавлено ребро $$$(i,j)$$$. Тогда $$$$$$ f(i,j)=\sum_{x=1}^{n}\left(\min_{y\in S_{i,j}}\mathrm{dis}_{i,j}(x,y)\right). $$$$$$
Дореми записала все значения $$$f(i,j)$$$ для $$$1 \leq j \leq i \leq n$$$, потом пошла спать. Однако проснувшись, она обнаружила, что дерево пропало. К счастью, значения $$$f(i,j)$$$ все еще в ее тетради, и она значит, каким $$$i$$$ и $$$j$$$ они соответствуют. Вам даны значения $$$f(i,j)$$$, можете ли вы помочь Дореми восстановить дерево?
Гарантируется, что хотя бы одно подходящее дерево существует.
Первая строка содержит одно целое число $$$n$$$ ($$$2 \le n \le 2000$$$) — количество вершин в дереве.
Следующие $$$n$$$ строк содержат нижне-треугольную матрицу с $$$i$$$ целыми числами в $$$i$$$-й строке; $$$j$$$-е число в $$$i$$$-й строке равно $$$f(i,j)$$$ ($$$0 \le f(i,j) \le 2\cdot 10^{15}$$$).
Гарантируется, что существует дерево, веса ребер которого являются целыми числами в пределах от $$$1$$$ до $$$10^9$$$ такое, что все значения $$$f(i,j)$$$ для этого дерева совпадают с данными.
Выведите $$$n-1$$$ строку, описывающую дерево. В $$$i$$$-й строке выведите три целых числа $$$u_i$$$, $$$v_i$$$, $$$w_i$$$ ($$$1 \le u_i,v_i \le n$$$, $$$1 \le w_i \le 10^9$$$), обозначающих ребро $$$(u_i,v_i)$$$ веса $$$w_i$$$.
Если существуют несколько решений, выведите любое из них.
Ребра должны образовывать дерево, а все значения $$$f(i,j)$$$ должны совпадать с данными.
3 7 3 5 0 2 8
2 3 3 1 2 2
9 8081910646 8081902766 8081903751 8081902555 8081903540 8081905228 3090681001 3090681986 3090681775 7083659398 7083657913 7083658898 7083658687 2092437133 15069617722 1748216295 1748217280 1748217069 5741194692 749972427 10439821163 2377558289 2377559274 2377559063 6370536686 1379314421 5028071980 8866466178 1746983932 1746984917 1746984706 5739962329 748740064 10438588800 5026839617 10448447704 2341942133 2341943118 2341942907 6334920530 1343698265 4992455824 8830850022 4991223461 9115779270
1 2 985 2 3 211 2 4 998244353 2 5 998244853 4 6 671232353 6 8 1232363 4 7 356561356 7 9 35616156
Для первого примере рисунок ниже слева направо сверху вниз показывает графы, получающиеся при добавлении ребер $$$(1,1)$$$, $$$(1,2)$$$, $$$(1,3)$$$, $$$(2,2)$$$, $$$(2,3)$$$, $$$(3,3)$$$ соответственно. Вершины на цикле выделены желтым.
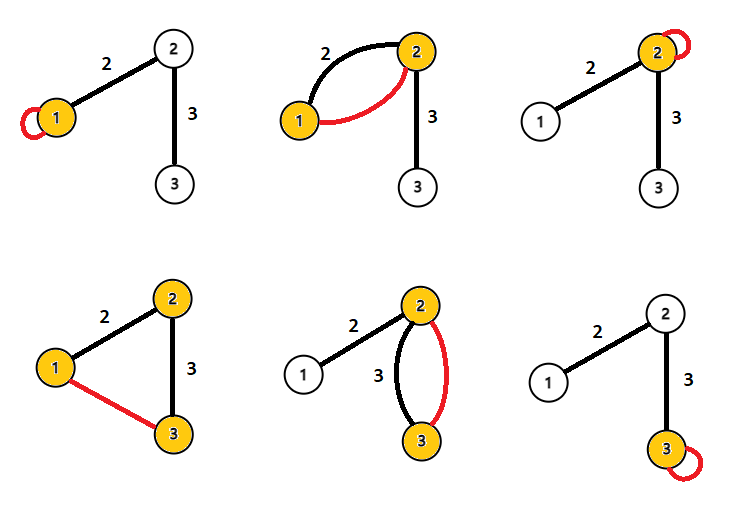
| Название |
|---|




