| Codeforces Round 826 (Div. 3) |
|---|
| Закончено |
Кирилл живёт на связном неориентированном графе из $$$n$$$ вершин и $$$m$$$ рёбер в вершине с номером $$$1$$$. В один прекрасный вечер он собрал у себя $$$f$$$ друзей, $$$i$$$-й друг живёт в вершине $$$h_i$$$. Таким образом, в настоящий момент все друзья находятся в вершине $$$1$$$, каждый должен добраться домой — $$$i$$$-й друг должен попасть в вершину $$$h_i$$$.
Вечер подошёл к концу и настала пора расходиться. Оказалось, что у $$$k$$$ ($$$k \le 6$$$) из его друзей нет машин и им придётся идти пешком, если их никто не подвезёт. Один друг с машиной может подвезти любое количество друзей без машин, но только если он может подвезти их, проехав по одному из кратчайших путей до своего дома.
Например, в графе ниже, друг из вершины $$$h_i=5$$$ может подвезти друзей из следующих наборов вершин: $$$[2, 3]$$$, $$$[2, 4]$$$, $$$[2]$$$, $$$[3]$$$, $$$[4]$$$, но не может подвезти друга из вершины $$$6$$$ или набор $$$[3, 4]$$$.
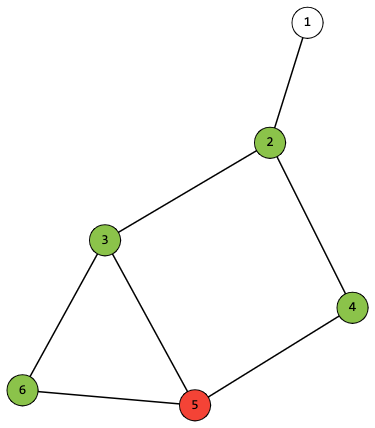 Вершины в которых живут друзья без машин выделены зелёным, а с машинами — красным.
Вершины в которых живут друзья без машин выделены зелёным, а с машинами — красным. Кирилл хочет, чтобы как можно меньшему числу друзей пришлось идти пешком. Помогите ему найти минимально возможное количество.
Первая строка входных данных содержит целое число $$$t$$$ ($$$1 \le t \le 10^3$$$) — количество наборов входных данных в тесте.
Первая строка набора содержит два целых числа $$$n$$$ и $$$m$$$ ($$$2 \le n \le 10^4$$$, $$$n-1 \le m \le min (10^4, $$$$$$ \frac{n \cdot (n - 1)}{2} $$$$$$)$$$) — количество вершин и рёбер соответственно.
Следующие $$$m$$$ строк набора содержат описание рёбер, по два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \ne v$$$) — номера вершин, соединённых ребром. Гарантируется, что в графе нет петель и кратных рёбер.
Дальше следует строка набора, содержащая число $$$f$$$ ($$$1 \le f \le 10^4$$$) — количество друзей Кирилла.
Следующая строка набора содержит $$$f$$$ целых чисел: $$$h_1, h_2, \dots, h_f$$$ ($$$2 \le h_i \le n$$$) — вершины, в которых они живут. Некоторые вершины могут повторяться.
Следующая строка набора содержит число $$$k$$$ ($$$1 \le k \le min(6, f)$$$) — количество друзей без машин.
Последняя строка каждого набора содержит $$$k$$$ целых чисел: $$$p_1, p_2, \dots, p_k$$$ ($$$1 \le p_i \le f$$$, $$$p_i < p_{i+1}$$$) — номера друзей без машин.
Гарантируется, что сумма $$$n$$$ по всем наборам не превосходит $$$10^4$$$, как и суммы $$$m$$$ и $$$f$$$.
Выведите $$$t$$$ строк, каждая из которых содержит ответ на соответствующий набор входных данных. В качестве ответа выведите единственное число — минимально возможное количество друзей, которым придётся идти пешком.
36 71 22 32 43 54 53 66 552 3 4 5 641 2 3 56 71 22 32 43 54 53 66 562 3 4 5 6 541 2 3 54 41 21 32 33 433 4 221 3
2 1 1
32 11 232 2 231 2 33 31 21 32 342 2 2 331 2 44 43 13 21 42 453 2 2 4 231 3 4
3 1 0
Первый набор входных данных первого примера разобран в условии.
Во втором наборе входных данных первого примера в вершине $$$5$$$ живут два друга с машинами, один может подвезти друзей из вершин $$$2$$$ и $$$3$$$, а второй из вершины $$$4$$$, не подвезут только друга из вершины $$$6$$$.
| Название |
|---|




