| Codeforces Round 826 (Div. 3) |
|---|
| Закончено |
Девочка Маша гуляла в лесу и нашла полное бинарное дерево высоты $$$n$$$ и перестановку $$$p$$$ длины $$$m=2^n$$$.
Полное бинарное дерево высоты $$$n$$$ — это такое корневое дерево, что каждая вершина кроме листьев имеет ровно двух сыновей, а длина пути от корня до любого из листьев равна $$$n$$$. Ниже на картинке изображено полное бинарное дерево для $$$n=2$$$.
Перестановкой называется массив, состоящий из $$$n$$$ различных целых чисел от $$$1$$$ до $$$n$$$. Например, [$$$2,3,1,5,4$$$] является перестановкой, а [$$$1,2,2$$$] не является ($$$2$$$ встречается дважды), и [$$$1,3,4$$$] тоже не является перестановкой ($$$n=3$$$, но в массиве есть $$$4$$$).
Пронумеруем $$$m$$$ листьев этого дерева слева направо. В листе с номером $$$i$$$ записано значение $$$p_i$$$ ($$$1 \le i \le m$$$).
Например, если $$$n = 2$$$, $$$p = [3, 1, 4, 2]$$$, дерево будет выглядеть так:
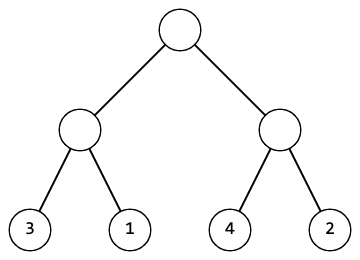
Маша считает дерево красивым, если значения в его листьях упорядочены слева направо по возрастанию.
За одну операцию Маша может выбрать произвольную не являющуюся листом вершину дерева и поменять местами ее левого и правого сына (вместе с их поддеревьями).
Например, если Маша применит эту операцию к корню рассмотренного выше дерева, оно приобретет следующий вид:
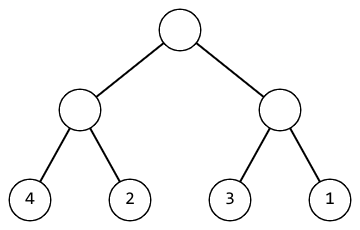
Помогите Маше понять, сможет ли она за некоторое количество операций сделать дерево красивым. Если сможет, то выведите минимальное количество операций, чтобы сделать дерево красивым.
В первой строке дано число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
В каждом наборе входных данных в первой строке дано целое число $$$m$$$ ($$$1 \le m \le 262144$$$), являющееся степенью двойки — размер перестановки $$$p$$$.
Во второй строке даны $$$m$$$ целых чисел: $$$p_1, p_2, \dots, p_m$$$ ($$$1 \le p_i \le m$$$) — перестановка $$$p$$$.
Гарантируется, что сумма значений $$$m$$$ по всем наборам входных данных не превосходит $$$3 \cdot 10^5$$$.
Для каждого набора входных данных в отдельной строке выведите минимальное возможное количество операций, за которое Маша сможет сделать дерево красивым или -1, если это невозможно.
486 5 7 8 4 3 1 243 1 4 21187 8 4 3 1 2 6 5
4 -1 0 -1
Рассмотрим первый тест.
В первом наборе входных данных можно действовать так (фиолетовым цветом выделена вершина, к которой на текущем шаге применяется операция):
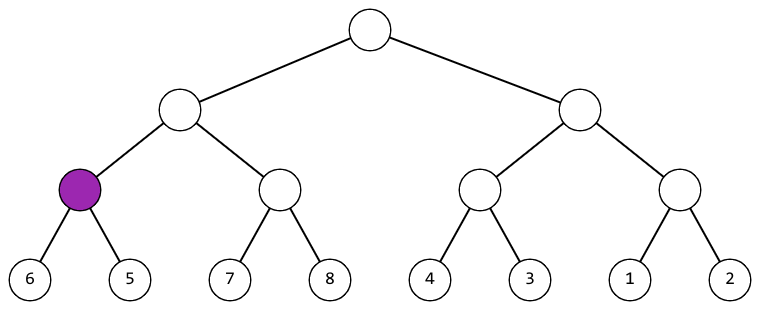 | 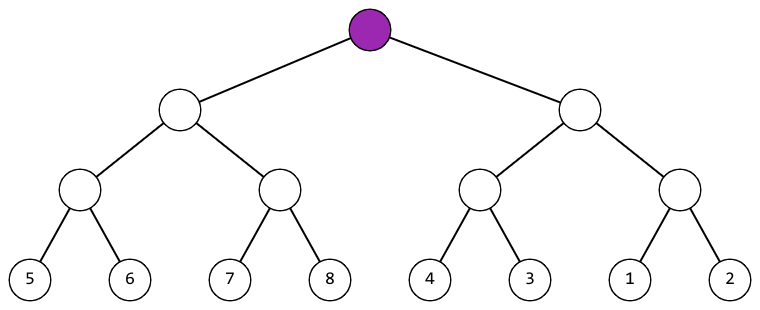 |
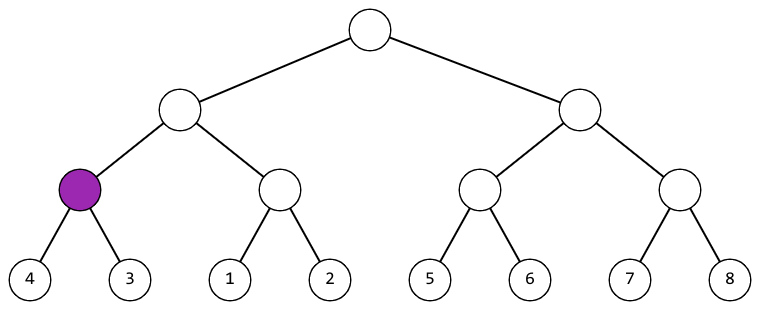 | 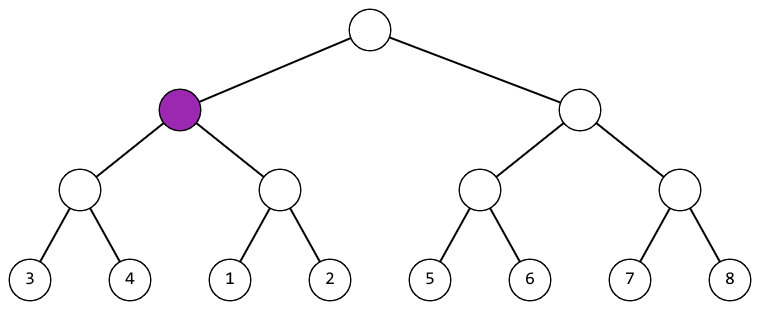 |
Во втором наборе входных данных можно показать, что нельзя сделать дерево красивым.
В третьем наборе входных данных дерево сразу является красивым.
| Название |
|---|




