| Codeforces Round 831 (Div. 1 + Div. 2) |
|---|
| Закончено |
У Пака Чанека есть сетка из порталов размера $$$n \times m$$$. Портал в $$$i$$$-й строке и $$$j$$$-м столбце обозначается как портал $$$(i,j)$$$. Порталы $$$(1,1)$$$ и $$$(n,m)$$$ находятся в северо-западном и юго-восточном углах сетки соответственно.
Портал $$$(i,j)$$$ имеет две настройки:
- Тип $$$t_{i,j}$$$, который может быть $$$0$$$ или $$$1$$$.
- Сила $$$s_{i,j}$$$, являющаяся целым числом от $$$1$$$ до $$$10^9$$$ включительно.
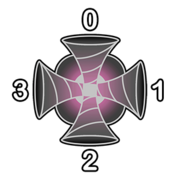
Когда лазерный луч входит в грань $$$k$$$ портала $$$(i, j)$$$ со скоростью $$$x_\text{in}$$$, он покидает портал из грани $$$(k+2+t_{i,j}) \bmod 4$$$ со скоростью $$$x_\text{out} = \max(x_\text{in},s_{i,j})$$$. Портал при этом потребляет $$$x_\text{out} - x_\text{in}$$$ единиц энергии.
Паку Чанеку сегодня очень скучно. Он собирается запустить $$$4nm$$$ лазерных лучей с начальной скоростью $$$1$$$, по одному в каждую грань каждого портала. Каждый луч будет перемещаться по этой сетке порталов, пока не выйдет за пределы сетки или не пройдет через $$$10^{100}$$$ порталов.
Пак Чанек считает, что портал хороший тогда и только тогда, когда суммарная энергия, потребленная этим порталом по модулю $$$2$$$, равна его типу. Учитывая настройки силы всех порталов, найдите способ назначить настройки типа каждого портала таким образом, чтобы количество хороших порталов было максимально возможным.
Первая строка содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n, m \le 1000$$$) — количество строк и столбцов в сетке.
В $$$i$$$-й из следующих $$$n$$$ строк содержатся $$$m$$$ целых чисел, $$$j$$$-е целое число — значение $$$s_{i,j}$$$ ($$$1 \leq s_{i,j} \leq 10^9$$$), сила портала $$$(i, j)$$$.
Выведите $$$n$$$ строк, каждая их которых состоит из $$$m$$$ символов $$$0$$$ или $$$1$$$, обозначающих тип портала, где $$$j$$$-й символ в $$$i$$$-й строке это настройка типа портала $$$(i, j)$$$.
Если решений несколько, выведите любое из них.
2 3 8 8 2 6 5 7
110 100
1 2 420 69
10
В первом примере рассмотрим лазерный луч, который Пак Чанек запускает в грань $$$1$$$ портала $$$(2, 2)$$$. Луч перемещается следующим образом:
- Луч входит в грань $$$1$$$ портала $$$(2, 2)$$$ со скоростью $$$1$$$. Он покидает портал из грани $$$3$$$ со скоростью $$$5$$$. Портал $$$(2, 2)$$$ потребляет $$$4$$$ единиц энергии.
- Луч входит в грань $$$1$$$ портала $$$(2, 1)$$$ со скоростью $$$5$$$. Он покидает портал из грани $$$0$$$ со скоростью $$$6$$$. Портал $$$(2, 1)$$$ потребляет $$$1$$$ единиц энергии.
- Луч входит в грань $$$2$$$ портала $$$(1, 1)$$$ со скоростью $$$6$$$. Он покидает портал из грани $$$1$$$ со скоростью $$$8$$$. Портал $$$(1, 1)$$$ потребляет $$$2$$$ единиц энергии.
- Луч входит в грань $$$3$$$ портала $$$(1, 2)$$$ со скоростью $$$8$$$. Он покидает портал из грани $$$2$$$ со скоростью $$$8$$$. Портал $$$(1, 2)$$$ потребляет $$$0$$$ единиц энергии.
- Луч входит в грань $$$0$$$ портала $$$(2, 2)$$$ со скоростью $$$8$$$. Он покидает портал из грани $$$2$$$ со скоростью $$$8$$$. Портал $$$(2, 2)$$$ потребляет $$$0$$$ единиц энергии.
Иллюстрация перемещений луча, описанных выше, выглядит следующим образом.
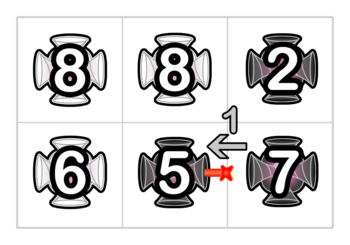
Для примера рассмотрим портал $$$(2, 3)$$$. Мы можем подсчитать, что суммарная энергия, потребляемая этим порталом, к концу процесса составит $$$32$$$. Так как $$$32 \bmod 2 = 0$$$ и $$$t_{2,3} = 0$$$, этот портал будет считаться хорошим.
| Название |
|---|




