| Codeforces Round 831 (Div. 1 + Div. 2) |
|---|
| Закончено |
У Пака Чанека есть $$$n$$$ двухмерных ломтиков сыра. $$$i$$$-й ломтик сыра можно представить в виде прямоугольника размерами $$$a_i \times b_i$$$. Мы хотим расположить их на двумерной плоскости так, чтобы:
- Каждая грань каждого ломтика сыра параллельна либо оси x, либо оси y.
- Нижняя грань каждого ломтика — это отрезок на оси x.
- Никакие два ломтика не пересекаются, но они могут соприкасаться гранями.
- Они образуют одну связанную фигуру.
Обратите внимание, что мы можем расположить их в любом порядке (крайний левый ломтик сыра не обязательно является первым ломтиком сыра). Также обратите внимание, что мы можем вращать каждый ломтик сыра любым способом при условии выполнения остальных ограничений.
Найдите минимально возможный периметр построенной фигуры.
Каждый тест содержит несколько наборов входных данных. Первая строка содержит целое число $$$t$$$ ($$$1 \leq t \leq 2 \cdot 10^4$$$) — количество наборов входных данных. Следующие строки содержат описания наборов входных данных.
Первая строка каждого набора входных данных содержит целое число $$$n$$$ ($$$1 \leq n \leq 2 \cdot 10^5$$$) — количество ломтиков сыра у Пака Чанека.
В $$$i$$$-й из следующих $$$n$$$ строк каждого набора содержатся два целых числа $$$a_i$$$ и $$$b_i$$$ ($$$1 \leq a_i,b_i \leq 10^9$$$) — размеры $$$i$$$-го ломтика сыра.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите строку, содержащую целое число — минимально возможный периметр построенной фигуры.
344 14 51 12 332 42 62 312 65
26 24 134
В первом наборе входных данных один из способов получения минимально возможного периметра выглядит следующим образом.

Мы можем вычислить периметр построенной фигуры: $$$2+5+1+1+1+1+3+1+5+1+2+3=26$$$. Можно показать, что нельзя получить меньший периметр.
Ниже показано некорректное расположение.
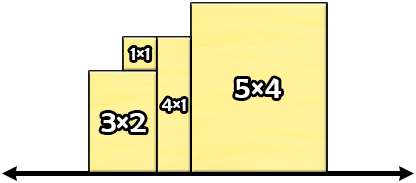
Периметр данной фигуры $$$24$$$, но не все ограничения в задаче выполнены. Нижняя грань ломтика $$$1 \times 1$$$ не находится на оси x.
Во втором наборе входных данных один из способов получения минимально возможного периметра выглядит следующим образом.
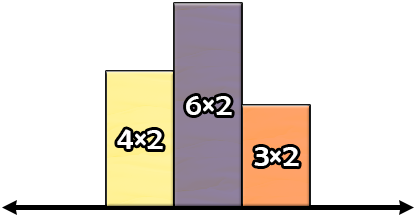
Мы можем вычислить периметр построенной фигуры: $$$2+2+2+3+2+3+2+2+2+4=24$$$. Можно показать, что нельзя получить меньший периметр.
| Название |
|---|




