| Dytechlab Cup 2022 |
|---|
| Закончено |

Эле нужно отправить большой пакет данных с компьютера $$$1$$$ на компьютер $$$n$$$ через сеть компьютеров. В настоящее время сеть работает слишком медленно, и пакет может не успеть вовремя. К счастью, добрый волшебник протянул ей руку помощи.
Сеть может быть представлена как неориентированный связный граф с $$$n$$$ вершинами, каждая из которых представляет компьютер. Для их соединения используются $$$m$$$ проводов. Провод $$$i$$$ используется для соединения компьютеров $$$u_i$$$ и $$$v_i$$$ и имеет вес $$$w_i$$$. Вышеупомянутый пакет при прохождении через провод $$$i$$$ переместится с компьютера $$$u_i$$$ на компьютер $$$v_i$$$ (или наоборот) ровно за $$$w_i$$$ микросекунд. Волшебник может использовать свое заклинание произвольное количество раз. Для каждого заклинания он выберет провод с индексом $$$i$$$, соединяющий компьютеры $$$u_i$$$ и $$$v_i$$$, и переподключит его, выполнив следующие действия:
- Выберет один из компьютеров, соединенный этим проводом. Без ограничения общности выберем $$$v_i$$$.
- Выберет компьютер, который в данный момент подключен к $$$v_i$$$ (можно выбрать $$$u_i$$$), назовем его $$$t_i$$$, отсоединит провод с индексом $$$i$$$ от $$$v_i$$$, и соединит им $$$u_i$$$ и $$$t_i$$$.
Переподключение провода $$$i$$$ займет $$$w_i$$$ микросекунд, а вес провода после этой операции не изменится. После переподключения компьютер может иметь какой-то провод, соединяющий его с самим собой. Переподключение также может сделать граф несвязным.
Задача Элы — как можно быстрее отправить пакет данных с компьютера $$$1$$$ на компьютер $$$n$$$. Обратите внимание, что волшебник может использовать свое заклинание сколько угодно раз (возможно, ноль). Чтобы обеспечить бесперебойную работу сети при передаче большого пакета, все заклинания могут использоваться только до начала передачи данных с компьютера $$$1$$$.
Какое минимальное количество времени потребуется для передачи пакета данных с компьютера $$$1$$$ на компьютер $$$n$$$, с учетом времени, потраченного на применение заклинаний?
Во входных данных находятся несколько наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 100$$$) — количество наборов входных данных. Далее следуют наборы входных данных.
В первой строке каждого набора заданы два целых числа $$$n$$$ и $$$m$$$ ($$$2 \le n \le 500$$$, $$$n - 1 \le m \le 250 000$$$) — количество вершин и проводов соответственно.
$$$i$$$-я из следующих $$$m$$$ строк содержит три числа $$$u_i$$$, $$$v_i$$$ и $$$w_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$1 \le w_i \le 10^9$$$) — номера двух компьютеров, соединенных $$$i$$$-м проводом, и его вес.
Гарантируется, что сумма $$$n$$$ по всем наборам не превышает $$$500$$$ и сумма $$$m$$$ по всем наборам не превышает $$$250 000$$$. Граф в каждом наборе входных данных гарантированно будет связным и без петель, но он может содержать кратные ребра.
Для каждого набора входных данных выведите одно целое число, обозначающее наименьшее количество времени, необходимое для передачи пакета данных с компьютера $$$1$$$ на $$$n$$$.
38 91 2 36 4 53 5 66 1 37 4 43 8 42 3 37 8 54 5 24 51 2 12 4 13 4 13 1 11 3 28 84 6 927 1 656 5 436 7 964 3 744 8 547 4 992 5 22
9 2 154
Граф в первом наборе входных данных:
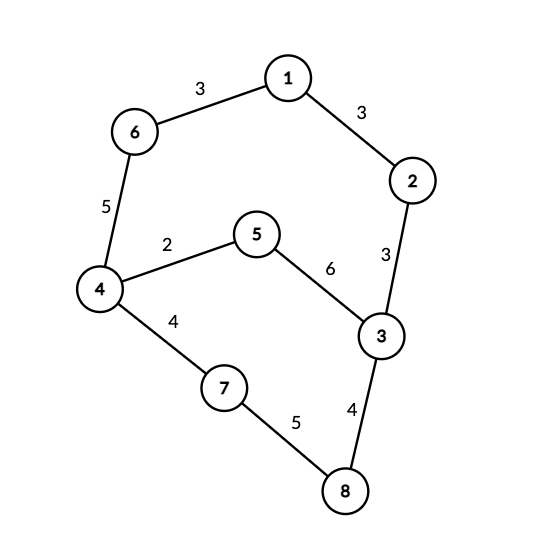
Эла может попросить волшебника использовать его заклинание на проводе с индексом $$$7$$$, который соединяет компьютеры $$$2$$$ и $$$3$$$. Поскольку компьютер $$$8$$$ подключена к компьютеру $$$3$$$, волшебник может отключить провод $$$7$$$ от компьютера $$$3$$$ и подключить его к компьютеру $$$8$$$ за $$$3$$$ микросекунды (вес провода $$$3$$$).
После этого пакет можно отправить с компьютера $$$1$$$ на компьютер $$$8$$$ за $$$6$$$ микросекунд. Следовательно, ответ $$$3 + 6 = 9$$$ микросекунд.
| Название |
|---|




