| Codeforces Round 820 (Div. 3) |
|---|
| Закончено |
Это интерактивная задача.
Я хочу сыграть с тобой в одну игру...
Мы загадали циклический граф из $$$n$$$ вершин ($$$3 \le n \le 10^{18}$$$). Циклическим называется неориентированный граф из $$$n$$$ вершин, образующих один цикл. Каждая вершина принадлежит циклу, то есть длина цикла (количество рёбер в нём) равна в точности $$$n$$$. Порядок вершин в цикле — произвольный.
Вы можете делать запросы следующего вида:
- «? a b», где $$$1 \le a, b \le 10^{18}$$$ и $$$a \neq b$$$. В ответ на запрос интерактор выведет в отдельной строке длину случайного из двух путей из вершины $$$a$$$ в вершину $$$b$$$, либо -1, если $$$\max(a, b) > n$$$. Один из двух путей интерактор выбирает равновероятно. Длина пути — это количество рёбер в нём.
Вы победите, если угадаете количество вершин в загаданном цикле (число $$$n$$$), сделав не больше $$$50$$$ запросов.
Обратите внимание, что интерактор реализован так, что для любой упорядоченной пары $$$(a, b)$$$, на запрос «? a b» он всегда возвращает одно и то же значение, независимо от количества таких запросов. Отметим, что на запрос «? b a» интерактор может дать другой ответ.
Вершины в графе расставлены случайно и их позиции заранее фиксированы.
В этой задаче запрещены взломы. Количество тестов у жюри равно $$$50$$$.
Вы можете сделать не более $$$50$$$ запросов. Чтобы сделать запрос, выведите в отдельной строке:
- «? a b», где $$$1 \le a, b \le 10^{18}$$$ и $$$a \neq b$$$. В ответ на запрос интерактор выведет в отдельной строке длину случайного простого пути из вершины $$$a$$$ в вершину $$$b$$$ (не путать с путем из $$$b$$$ в $$$a$$$), либо $$$-1$$$, если $$$\max(a, b) > n$$$. Один из двух путей интерактор выбирает равновероятно.
Если в результате запроса вашей программой будет получено число 0, то это означает, что вердикт для вашего решения уже определён как «Неправильный ответ» (например, вы сделали больше $$$50$$$ запросов или совершили некорректный запрос). В этом случае ваша программа должна немедленно завершить свою работу. В противном случае в этом сценарии вы можете получить случайный вердикт «Ошибка исполнения», «Превышено ограничение времени» или какой-то другой вместо вердикта «Неправильный ответ».
Ответ, как и запросы, выведите в отдельной строке. Вывод ответа не считается запросом при подсчёте их количества. Чтобы вывести его, используйте следующий формат:
- «! n»: предполагаемую длину загаданного цикла ($$$3 \le n \le 10^{18}$$$).
После этого ваша программа должна завершить работу.
После вывода очередного запроса обязательно используйте функции очистки потока, чтобы часть вашего вывода не осталась в каком-нибудь буфере. Например, на С++ надо использовать функцию fflush(stdout), на Java вызов System.out.flush(), на Pascal flush(output) и stdout.flush() для языка Python.
Обратите внимание, что интерактор реализован так, что для любой упорядоченной пары $$$(a, b)$$$, на запрос «? a b» он всегда возвращает одно и то же значение, независимо от количества таких запросов. Отметим, что на запрос «? b a» интерактор может дать другой ответ.
Вершины в графе расставлены случайно и их позиции заранее фиксированы.
В этой задаче запрещены взломы. Количество тестов у жюри равно $$$50$$$.
1 2 -1
? 1 2 ? 1 3 ? 1 4 ! 3
В первом примере цикл может выглядеть следующим образом:
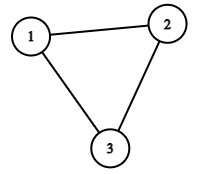
Длины простых путей между всеми парами вершин в данном случае равны $$$1$$$ или $$$2$$$.
- Первым запросом мы узнаем, что один из простых путей из вершины $$$1$$$ в вершину $$$2$$$ имеет длину $$$1$$$.
- Вторым запросом мы узнаем, что один из простых путей из вершины $$$1$$$ в вершину $$$3$$$ имеет длину $$$2$$$.
- Третьим запросом мы узнаем, что вершины $$$4$$$ нет в графе. Следовательно, размер графа равен $$$3$$$.
| Название |
|---|




