| Codeforces Round 818 (Div. 2) |
|---|
| Закончено |
Мадоке решили доверить организацию крупного турнира по компьютерной игре «OSU»!
В данном турнире матчи проходят по «олимпийской системе». Другими словами, в турнире участвуют $$$2^n$$$ участников, пронумерованных целыми числами от $$$1$$$ до $$$2^n$$$. Всего в турнире происходит $$$n$$$ раундов. В $$$i$$$-м раунде проходят $$$2^{n - i}$$$ матчей между двумя игроками (один из которых правый, другой левый), после которых победители проходят дальше по турнирной сетке, а проигравшие участники выбывают из турнира. При этом относительный порядок в следующем раунде не меняется. А победитель в турнире — последний оставшийся участник.
Но чем меньше номер участника, тем больше он заплатит Мадоке в случае победы, поэтому Мадока хочет, чтобы победил участник с наименьшим номером. Для этого она может как угодно расставить участников в первом раунде, а также для каждого матча определить кто победит — участник слева или справа.
Но Мадока знает, что спонсоры турнира могут не более $$$k$$$ раз поменять победителя в матчах. (То есть если до изменения побеждал участник слева, то после изменения будет побеждать участник справа, а если побеждал участник справа, то после изменения будет побеждать участник слева).
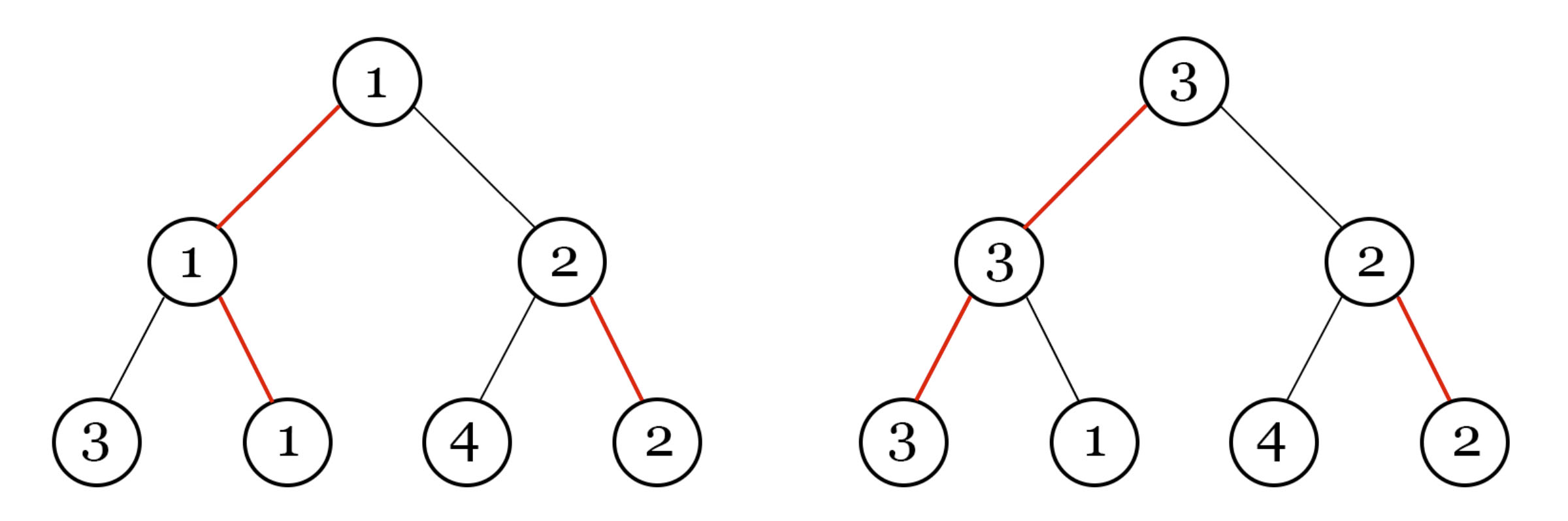 Так, на первом изображении показана турнирная сетка, которую сделала Мадока, где красные линии показывают, кто должен победить в матче. А на втором показана турнирная сетка, после одного измения исхода матча спонсорами (матч между игроками $$$1$$$ и $$$3$$$).
Так, на первом изображении показана турнирная сетка, которую сделала Мадока, где красные линии показывают, кто должен победить в матче. А на втором показана турнирная сетка, после одного измения исхода матча спонсорами (матч между игроками $$$1$$$ и $$$3$$$). Выведите минимально возможный номер победителя в турнире, который Мадока может гарантированно получить вне зависимости от изменений спонсоров. Но так как ответ может быть очень большим выведите его по модулю $$$10^9 + 7$$$. Обратите внимание, нам нужно минимизировать ответ, а только потом взять его по модулю.
В первой и единственной строке заданы два целых числа $$$n$$$ и $$$k$$$ ($$$1 \le n \le 10^5, 1 \le k \le \min(2^n - 1, 10^9)$$$) — количество раундов в турнире и количество исходов, которые спонсоры могут изменить.
Выведите ровно одно целое число — минимальный номер победителя по модулю $$$10^9 + 7$$$
1 1
2
2 1
3
3 2
7
В первом примере проходит всего один матч между игроками $$$1$$$ и $$$2$$$, поэтому спонсоры всегда смогут сделать так, чтобы выигрывал игрок $$$2$$$.
Схема турнира из второго примера изображена на картинке в условии.
| Название |
|---|




