| Codeforces Round 816 (Div. 2) |
|---|
| Закончено |
Это интерактивная задача.
Фермер Сережа выращивает кукурузу на прямоугольном поле $$$ n \times m $$$ метров c углами в точках с координатами $$$(0, 0)$$$, $$$(0, m)$$$, $$$(n, 0)$$$, $$$(n, m)$$$. В этом году урожай был обилен и кукуруза покрыла все поле.
Но в ночь перед сбором урожая прилетели инопланетяне и отравили кукурузу на поле в одном квадрате $$$1 \times 1$$$ метр со сторонами, параллельными границам поля. Кукурузу, попавшую внутрь квадрата, ни в коем случае нельзя есть, но отличить ее от обычной невооруженным взглядом невозможно. Можно только собрать пробу кукурузы с любого многоугольника и отдать в лабораторию, где ее проанализируют и скажут, сколько кукурузы было отравлено. Так как урожай скоро испортится, можно провести такое исследование не более $$$5$$$ раз.
Более формально, разрешено сделать не более $$$5$$$ запросов, каждым из которых можно узнать площадь пересечения любого выбранного многоугольника с инопланетянами квадратом. Необходимо узнать координаты левого нижнего угла квадрата отравленной кукурузы (вершину квадрата с наименьшими $$$x$$$ и $$$y$$$ координатами).
Первая строка содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n, m \le 100$$$) — размеры поля.
Для того, чтобы узнать площадь пересечения многоугольника с $$$k$$$ ($$$3 \le k \le 1000$$$) вершинами в точках с координатами $$$(x_1, y_1),\; \dots ,\;(x_k, y_k)$$$ с квадратом отравленной кукурузы выведите $$$k+1$$$ строку. В первой из этих строк выведите «? k». В $$$i$$$-й из следующих $$$k$$$ строк выведите два вещественных числа $$$x_i$$$ и $$$y_i$$$ ($$$|x_i|, |y_i| \le 10^4$$$) с не более $$$15$$$ знаками после запятой.
Многоугольник должен иметь строго положительную площадь и не иметь самопересечений.
В ответ на данный запрос вы получите действительное число $$$s$$$ ($$$0 \le s \le 1$$$) с $$$15$$$ знаками после запятой — площадь пересечения квадрата с заданным многоугольником. Если многоугольник некорректен, корректный ответ не гарантируется.
Когда вы определили отравленный квадрат, выведите в отдельной строке «! x y», где $$$x$$$ и $$$y$$$ — вещественные числа с не более $$$15$$$ знаками после запятой, описывающие координаты его левого нижнего угла ($$$0 \le x \le n - 1$$$, $$$0 \le y \le m - 1$$$) , и после этого ваша программа должна немедленно завершиться.
Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка по обеим координатам не превосходит $$$10^{-6}$$$. Формально, пусть ваш ответ равен $$$a$$$, а ответ жюри равен $$$b$$$. Ваш ответ будет зачтен, если $$$\frac{|a-b|}{max(1,|b|)} \le 10^{-6}$$$.
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт «Решение зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в С++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы
Для взлома задачи используйте следующий формат теста.
В первой строке входных данных должны содержаться два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n,m \le 100$$$) — размеры поля.
Во второй строке должны содержаться два вещественных числа $$$x$$$ и $$$y$$$ ($$$0 \le x \le n - 1$$$, $$$0 \le y \le m - 1$$$) — координаты левого нижнего угла отравленного квадрата.
3 3 0.5 0.5
? 4 0 0 2 0 2 3 0 3 ? 4 0 0 0 1 3 1 3 0 ! 1.5 0.5
В первом тесте из условия инопланетяне отравили квадрат с вершинами в точках с координатами $$$(1.5, 0.5)$$$, $$$(1.5, 1.5)$$$, $$$(2.5, 1.5)$$$, $$$(2.5, 0.5)$$$. На картинке он отмечен красным цветом, многоугольник, выбранный в запросе — синим, а их пересечение — зелёным.
Картинка к первому запросу:
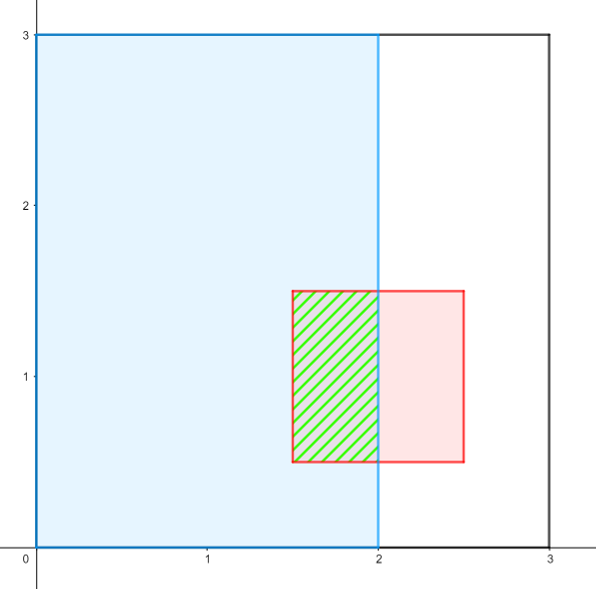
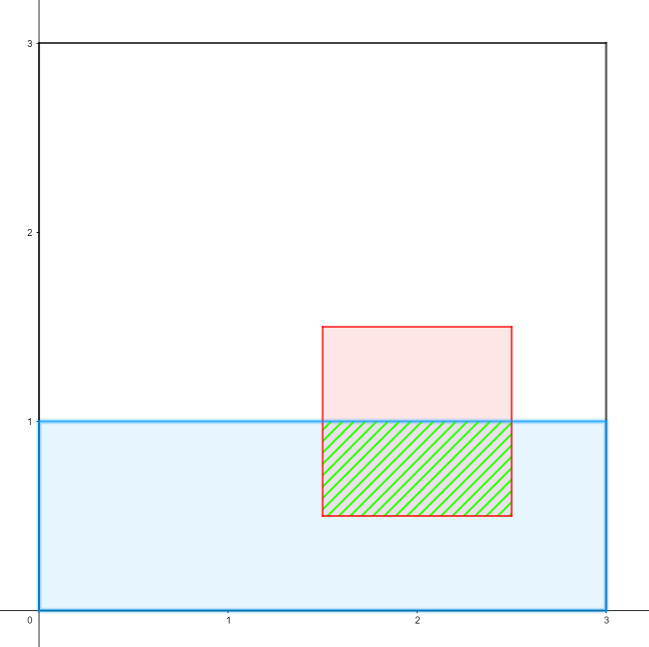
Картинка ко второму запросу:
| Название |
|---|




