| Codeforces Round 810 (Div. 1) |
|---|
| Закончено |
Вы владеете полем, который можно представить как бесконечную числовую прямую, все позиции на которой отмечены целыми числами.
В следующие $$$n$$$ дней будет идти дождь. В $$$i$$$-й день центр дождя будет располагаться в точке $$$x_i$$$, а интенсивность дождя будет равна $$$p_i$$$. Из-за дождей будет собираться дождевая вода; пусть $$$a_j$$$ будет обозначать объем воды, накопившийся в точке $$$j$$$. Изначально $$$a_j$$$ равно $$$0$$$, после дождя в $$$i$$$-й день это значение увеличится на $$$\max(0,p_i-|x_i-j|)$$$.
Поле затопит, если в некоторый момент будет существовать точка $$$j$$$, в которой накопится $$$a_j>m$$$ воды.
Вы можете использовать заклинание и отменить дождь в ровно один из дней, т. е. установить $$$p_i=0$$$. Для каждого $$$i$$$ от $$$1$$$ до $$$n$$$ определите, если вы отмените дождь в $$$i$$$-й день, верно ли, что затопления не случится?
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \leq n \leq 2 \cdot 10^5$$$, $$$1 \leq m \leq 10^9$$$) — количество дней и максимальный объем воды, который может находиться в одной точке, не вызывая затопления.
Далее следуют $$$n$$$ строк. $$$i$$$-я из этих строк содержит два целых числа $$$x_i$$$ и $$$p_i$$$ ($$$1 \leq x_i,p_i \leq 10^9$$$) — положение центра и интенсивность дождя в $$$i$$$-й день.
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите бинарную строку $$$s$$$ длины $$$n$$$. $$$i$$$-й символ строки $$$s$$$ должен быть равен 1, если в случае отмены дождя в $$$i$$$-й день затопления не случится, и 0, если в случае отмены дождя в $$$i$$$-й день затопление произойдет.
43 61 55 53 42 31 35 22 51 610 66 124 51 612 55 59 78 3
001 11 00 100110
В первом наборе входных данных, если не использовать заклинание, собравшаяся вода будет выглядеть следующим образом:
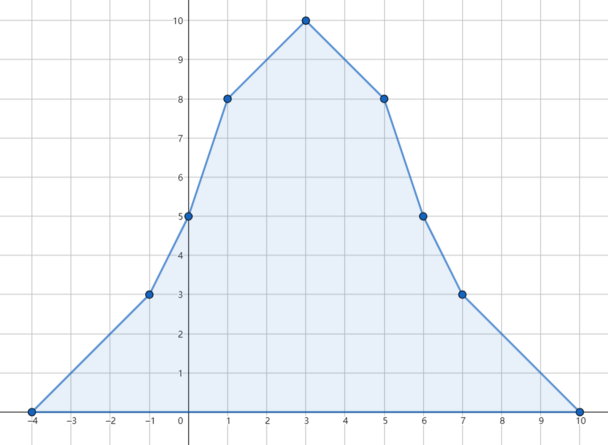
Если отменить дождь в третий день, затопление будет предотвращено, и собравшаяся вода будет выглядеть следующим образом:
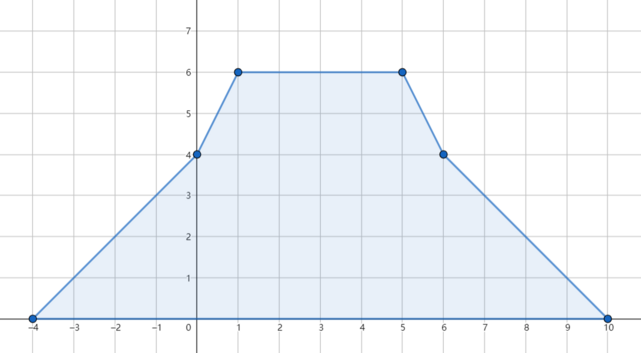
Во втором примере изначально нет затопления, поэтому можно отменить дождь в любой день.
В третьем примере нет способа избежать затопления.
| Название |
|---|




