| Codeforces Round 809 (Div. 2) |
|---|
| Закончено |
Qpwoeirut занялся архитектурой и решил перестроить свой город.
Город состоит из $$$n$$$ зданий, расположенных в ряд. Здание $$$i$$$ ($$$1 \le i \le n$$$) имеет высоту $$$h_i$$$ этажей. Вы можете считать, что все этажи в этой задаче имеют одинаковую высоту. Иными словами, здание $$$i$$$ выше здания $$$j$$$ тогда и только тогда, когда количество этажей $$$h_i$$$ в здании $$$i$$$ больше количества этажей $$$h_j$$$ в здании $$$j$$$.
Здание $$$i$$$ классное, если оно выше ($$$i-1$$$)-го здания и ($$$i+1$$$)-го здания одновременно (и оба этих здания существуют). В частности, $$$1$$$-е и $$$n$$$-е здания не могут быть классными.
Qpwoeirut хочет максимизировать количество классных зданий. Чтобы сделать это, он может строить новые этажи на уже существующих зданиях, тем самым делая их выше. Обратите внимание, что Qpwoeirut не может удалять уже существующие этажи.
Так как новые этажи очень дорогие, Qpwoeirut хочет минимизировать количество новых этажей. Найдите минимальное количество этажей, которое ему придётся построить, чтобы максимизировать количество классных зданий.
В первой строке задано одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следуют описания этих наборов.
В первой строке дано одно число $$$n$$$ ($$$3 \le n \le 10^5$$$) — количество зданий в городе.
Во второй строке даны $$$n$$$ целых чисел $$$h_1, h_2, \ldots, h_n$$$ ($$$1 \le h_i \le 10^9$$$) — высоты зданий в этажах.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите одно число: минимальное количество этажей, которое Qpwoeirut должен построить, чтобы максимизировать количество классных зданий.
632 1 251 2 1 4 363 1 4 5 5 284 2 1 3 5 3 6 161 10 1 1 10 181 10 11 1 10 11 10 1
2 0 3 3 0 4
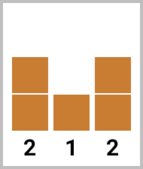
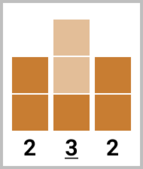
В первом наборе входных данных оптимально построить $$$2$$$ новых этажа на втором здании, в результате чего оно станет выше обоих соседних зданий. Высоты зданий будут равны $$$[2, \underline{3}, 2]$$$.
 |  |  |
Во втором наборе входных данных количество классных зданий уже максимально, поэтому Qpwoeirut может ничего не делать.
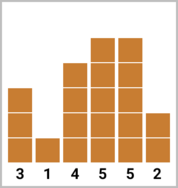
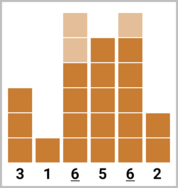
В третьем наборе входных данных оптимально построить $$$2$$$ этажа на третьем здании и $$$1$$$ этаж на пятом здании. Количество классных зданий будет равно двум. Высоты зданий будут равны $$$[3, 1, \underline{6}, 5, \underline{6}, 2]$$$.
 |  |  |
Можно показать, что нельзя сделать более $$$2$$$ классных зданий или сделать $$$2$$$ классных здания, построив не более $$$3$$$ этажей.
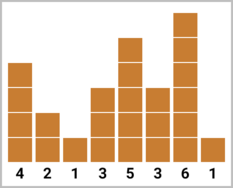
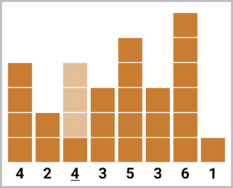
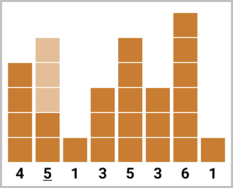
В четвёртом наборе входных данных можно сделать классным второе либо третье здание. В обоих случаях надо построить $$$3$$$ новых этажа. Высоты зданий будут равны $$$[4, 2, \underline{4}, 3, 5, 3, 6, 1]$$$ либо $$$[4, \underline{5}, 1, 3, 5, 3, 6, 1]$$$.
 |  |  |  |
| Название |
|---|




