| Codeforces Round 806 (Div. 4) |
|---|
| Закончено |
Вам дана квадратная матрица из $$$n$$$ строк и $$$n$$$ столбцов. В каждой ячейке содержится одно число: $$$0$$$ или $$$1$$$.
За одну операцию вы можете выбрать любую ячейку матрицы и инвертировать её значение ($$$0 \to 1$$$ или $$$1 \to 0$$$).
Найдите за какое минимальное число операций можно получить квадрат который не меняется при поворотах на $$$0^{\circ}$$$, $$$90^{\circ}$$$, $$$180^{\circ}$$$ и $$$270^{\circ}$$$.
На картинке ниже показан пример всех поворотов одной матрицы.
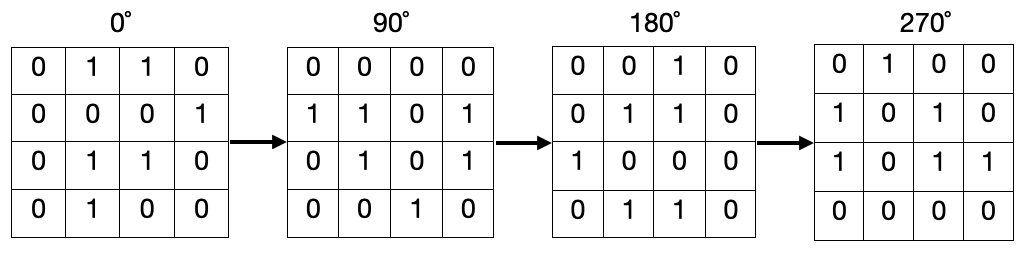
Первая строка содержит одно целое число $$$t$$$ ($$$1 \leq t \leq 100$$$) — количество наборов входных данных. Далее следует описание наборов.
Первая строка каждого набора входных данных содержит число $$$n$$$ ($$$1 \leq n \leq 100$$$) — размер матрицы.
Следующие $$$n$$$ строк каждого набора входных данных содержат строку длины $$$n$$$, состоящую из значений $$$a_{i,j}$$$ ($$$0 \leq a_{i,j} \leq 1$$$) — числа, записанные в каждой ячейке.
Для каждого набора входных данных выведите одно число — минимальное количество операций необходимое чтобы получить квадратную матрицу, которая не меняется при поворотах на $$$0^{\circ}$$$, $$$90^{\circ}$$$, $$$180^{\circ}$$$ и $$$270^{\circ}$$$.
5301011001010511100110110101110011110005010001010101010000100100151100100000111111011001111
1 0 9 7 6
В первом наборе входных данных, мы можем применить одну операцию чтобы сделать матрицу симметричной $$$\begin{matrix}0 & 1 & 0\\ 1 & 1 & \color{red}{1}\\ 0 & 1 & 0\end{matrix}$$$. Теперь, любой поворот не меняет данную матрицу.
Во втором наборе входных данных, нет необходимости применять ни одной операции, любые допустимые повороты и так не меняют её.
| Название |
|---|




