| Codeforces Global Round 21 |
|---|
| Закончено |
Перестановкой является массив, состоящий из $$$n$$$ различных целых чисел от $$$1$$$ до $$$n$$$ в произвольном порядке. Например, $$$[2,3,1,5,4]$$$ — перестановка, но $$$[1,2,2]$$$ не перестановка ($$$2$$$ встречается в массиве дважды) и $$$[1,3,4]$$$ тоже не перестановка ($$$n=3$$$, но в массиве встречается $$$4$$$).
Дана перестановка $$$[a_1,a_2,\dots,a_n]$$$ чисел $$$1,2,\dots,n$$$. Для целых $$$i$$$,$$$j$$$, таких что $$$1\le i<j\le n$$$, определим $$$\operatorname{mn}(i,j)$$$ как $$$\min\limits_{k=i}^j a_k$$$, а $$$\operatorname{mx}(i,j)$$$ как $$$\max\limits_{k=i}^j a_k$$$.
Построим неориентированный граф на $$$n$$$ вершинах, пронумерованных от $$$1$$$ до $$$n$$$. Для каждой пары $$$1\le i<j\le n$$$, если одновременно $$$\operatorname{mn}(i,j)=a_i$$$ и $$$\operatorname{mx}(i,j)=a_j$$$, или одновременно $$$\operatorname{mn}(i,j)=a_j$$$ и $$$\operatorname{mx}(i,j)=a_i$$$, то между вершинами $$$i$$$ и $$$j$$$ проводится неориентированное ребро длины $$$1$$$.
Найдите в этом графе длину кратчайшего пути от вершины $$$1$$$ до вершины $$$n$$$. Можно доказать, что в таком графе вершины $$$1$$$ и $$$n$$$ всегда будут соединены каким-либо путём, так что кратчайший путь всегда существует.
Во входных данных находятся несколько наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 5\cdot 10^4$$$) — количество наборов входных данных. Далее следуют наборы входных данных.
Первая строка набора входных данных содержит одно целое число $$$n$$$ ($$$1\le n\le 2.5\cdot 10^5$$$).
Вторая строка набора входных данных содержит $$$n$$$ целых чисел $$$a_1$$$,$$$a_2$$$,$$$\ldots$$$,$$$a_n$$$ ($$$1\le a_i\le n$$$). Гарантируется, что $$$a$$$ является перестановкой чисел $$$1$$$,$$$2$$$,$$$\dots$$$,$$$n$$$.
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$5\cdot 10^5$$$.
Для каждого набора входных данных выведите одно число — длину кратчайшего пути от $$$1$$$ до $$$n$$$.
51121 251 4 2 3 552 1 5 3 4107 4 8 1 6 10 3 5 2 9
0 1 1 4 6
Ниже приведены построенные графы, отвечающие наборам входных данных.
 граф в наборе 1
граф в наборе 1 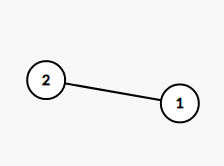 граф в наборе 2
граф в наборе 2 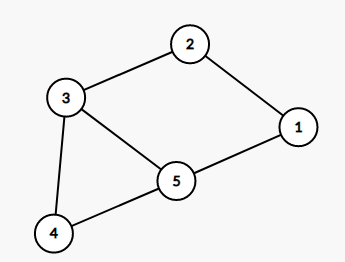 граф в наборе 3
граф в наборе 3 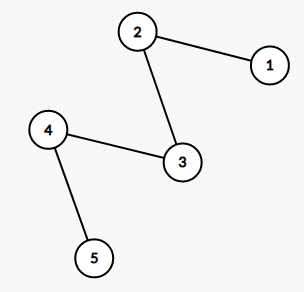 граф в наборе 4
граф в наборе 4 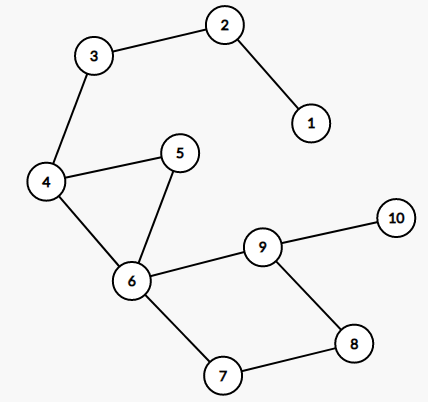 граф в наборе 5
граф в наборе 5
| Название |
|---|




