Вам дана таблица с $$$n$$$ строк и $$$m$$$ столбцов. Обозначим ячейку в $$$i$$$-й ($$$1\le i\le n$$$) строке и $$$j$$$-м ($$$1\le j\le m$$$) столбце через $$$(i, j)$$$, а число в ней через $$$a_{ij}$$$. Все числа равны $$$1$$$ или $$$-1$$$.
Вы начинаете с ячейки $$$(1, 1)$$$ и можете перемещаться на одну ячейку вниз или вправо за один раз. В конце концов, вы хотите оказаться в ячейке $$$(n, m)$$$.
Можно ли двигаться таким образом, чтобы сумма значений, записанных во всех посещенных ячейках (включая $$$a_{11}$$$ и $$$a_{nm}$$$), была равна $$$0$$$?
Каждый тест содержит несколько наборов входных данных. Первая строка содержит количество наборов входных данных $$$t$$$ ($$$1 \leq t \leq 10^4$$$). Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n, m \le 1000$$$) — размер таблицы.
Каждая из следующих $$$n$$$ строк содержит $$$m$$$ целых чисел. $$$j$$$-е целое число в $$$i$$$-й строке это $$$a_{ij}$$$ ($$$a_{ij} = 1$$$ или $$$-1$$$) — элемент в ячейке $$$(i, j)$$$.
Гарантируется, что сумма $$$n\cdot m$$$ по всем наборам входных данных не превышает $$$10^6$$$.
Для каждого набора входных данных выведите «YES», если существует путь из левого верхнего угла в правый нижний, который дает в сумме $$$0$$$, и «NO» в противном случае. Вы можете выводить каждую букву в любом регистре.
51 111 21 -11 41 -1 1 -13 41 -1 -1 -1-1 1 1 -11 1 1 -13 41 -1 1 1-1 1 -1 11 -1 1 1
NO YES YES YES NO
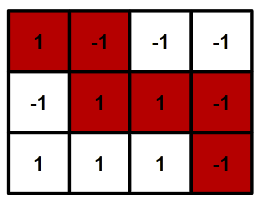
Один из возможных путей для четвертого набора входных данных приведен на рисунке в утверждении.
| Название |
|---|




