Майкл и Джо играют в игру. Игра ведется в табличке с $$$n$$$ строками и $$$m$$$ столбцами, заполненной попарно различными целыми числами. Обозначим ячейку в $$$i$$$-й ($$$1\le i\le n$$$) строке и $$$j$$$-м ($$$1\le j\le m$$$) столбце через $$$(i, j)$$$, а число в ней через $$$a_{ij}$$$.
Майкл начинает с того, что называет два числа $$$h$$$ ($$$1\le h \le n$$$) и $$$w$$$ ($$$1\le w \le m$$$). Затем Джо выбирает любой подпрямоугольник доски размером $$$h\times w$$$ (так, чтобы Майкл не видел).
Формально, подпрямоугольник $$$h\times w$$$ начинается с некоторой ячейки $$$(a,b)$$$, где $$$1 \le a \le n-h+1$$$ и $$$1 \le b \le m-w+1$$$. Он содержит все ячейки $$$(i,j)$$$ с $$$a \le i \le a+h-1$$$ и $$$b \le j \le b+w-1$$$.
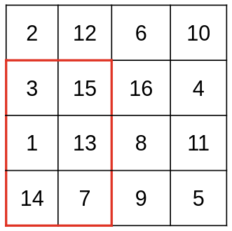Возможный ход Джо, если Майкл скажет $$$3\times 2$$$ (с максимумом в $$$15$$$). Наконец, Майкл должен угадать максимальное число в выбранном подпрямоугольнике. Он выигрывает, если угадает правильно.
Так как Майкл не любит большие числа, он хочет, чтобы площадь выбранного подпрямоугольника (то есть $$$h \cdot w$$$) была как можно меньше, но чтобы при этом он мог выиграть, независимо от выбора Джо. Помогите Майклу найти эту минимально возможную площадь.
Можно показать, что Майкл всегда может выбрать $$$h, w$$$, для которых он может гарантировать свой выигрыш.
Каждый тест содержит несколько наборов входных данных. Первая строка содержит количество наборов входных данных $$$t$$$ ($$$1 \le t \le 20$$$). Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n, m \le 40$$$) — размер таблицы.
Каждая из следующих $$$n$$$ строк содержит $$$m$$$ целых чисел. $$$j$$$-е целое число в $$$i$$$-й строке это $$$a_{ij}$$$ ($$$-10^9 \le a_{ij} \le 10^9$$$) — элемент в ячейке $$$(i, j)$$$.
Гарантируется, что все числа попарно различны (то есть, если $$$a_{i_1j_1} = a_{i_2j_2}$$$, то $$$i_1 = i_2, j_1 = j_2$$$).
Для каждого набора входных данных выведите одно целое положительное число — минимально возможную площадь подпрямоугольника, при которой Майкл может гарантировать победу.
31 134 42 12 6 103 15 16 41 13 8 1114 7 9 52 3-7 5 20 8 -3
1 9 4
В первом примере таблица имеет размер $$$1\times 1$$$, поэтому единственным возможным выбором для $$$h, w$$$ является $$$h = 1, w = 1$$$, что дает площадь $$$h\cdot w = 1$$$.
Таблица из второго набора входных данных нарисована в условии. Можно показать, что при $$$h = 3, w = 3$$$ Майкл может гарантировать победу и что любой выбор с $$$h\cdot w \le 8$$$ победы не гарантирует.
