| Codeforces Round 797 (Div. 3) |
|---|
| Закончено |
Дано число $$$n$$$ — количество доступных блоков. Необходимо использовать все блоки, чтобы построить пьедестал.
Пьедестал состоит из $$$3$$$-х платформ для $$$2$$$-го, $$$1$$$-го и $$$3$$$-го мест соответственно. При этом платформа для $$$1$$$-го места должна быть строго выше, чем для $$$2$$$-го места, а платформа для $$$2$$$-го места должна быть строго выше, чем для $$$3$$$-го. А также, высота каждой платформы должна быть больше нуля (то есть каждая платформа должна содержать хотя бы один блок).
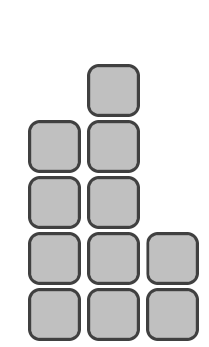 Пример пьедестала из $$$n=11$$$ блоков: высота второго места равна $$$4$$$ блокам, высота первого места равна $$$5$$$ блокам, высота третьего места равна $$$2$$$ блокам.
Пример пьедестала из $$$n=11$$$ блоков: высота второго места равна $$$4$$$ блокам, высота первого места равна $$$5$$$ блокам, высота третьего места равна $$$2$$$ блокам.Среди всех возможных пьедесталов из $$$n$$$ блоков выведите такой, что высота платформы для $$$1$$$-го места минимальна. Если таких несколько, выведите любой из них.
В первой строке входных данных дано целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
В каждом наборе входных данных содержится единственное целое число $$$n$$$ ($$$6 \le n \le 10^5$$$) — суммарное количество блоков для пьедестала. Необходимо использовать все $$$n$$$ блоков.
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$10^6$$$.
Для каждого набора входных данных выведите $$$3$$$ числа $$$h_2, h_1, h_3$$$ — высоты платформ для $$$2$$$-го, $$$1$$$-го и $$$3$$$-го мест на пьедестале, состоящем из $$$n$$$ блоков ($$$h_1+h_2+h_3=n$$$, $$$0 < h_3 < h_2 < h_1$$$).
Среди всех возможных пьедесталов выведите тот, для которого значение $$$h_1$$$ минимально. Если таких несколько, выведите любой из них.
61161010000078
4 5 2 2 3 1 4 5 1 33334 33335 33331 2 4 1 3 4 1
В первом наборе входных данных мы не можем получить высоту платформы для первого места меньше $$$5$$$, так как если высота платформы для первого места не больше $$$4$$$, то мы можем использовать максимум $$$4 + 3 + 2 = 9$$$ блоков. А должны использовать $$$11 = 4 + 5 + 2$$$ блоков. Поэтому ответ 4 5 2 подходит.
Во втором наборе единственный подходящий ответ: 2 3 1.
| Название |
|---|




