| Codeforces Round 793 (Div. 2) |
|---|
| Закончено |
Вам даны два массива $$$a$$$ и $$$b$$$ целых чисел ($$$b_i \neq 0$$$ и $$$|b_i| \leq 10^9$$$). Массив $$$a$$$ отсортирован в неубывающем порядке.
Стоимость подмассива $$$a[l:r]$$$ определяется следующим образом:
Если $$$ \sum\limits_{j = l}^{r} b_j \neq 0$$$, то стоимость не определена.
Иначе:
- Постройте двудольный поточный граф с $$$r-l+1$$$ вершинами, помеченными от $$$l$$$ до $$$r$$$, причем все вершины с $$$b_i \lt 0$$$ расположены слева, а с $$$b_i \gt 0$$$ — справа. Для каждых $$$i, j$$$ таких, что $$$l \le i, j \le r$$$, $$$b_i<0$$$ и $$$b_j>0$$$, нарисуйте ребро от $$$i$$$ к $$$j$$$ с бесконечной пропускной способностью и стоимостью единицы потока равной $$$|a_i-a_j|$$$.
- Добавьте еще две вершины: источник $$$S$$$ и сток $$$T$$$.
- Для каждого $$$i$$$ такого, что $$$l \le i \le r$$$ и $$$b_i<0$$$, добавьте ребро от $$$S$$$ к $$$i$$$ со стоимостью $$$0$$$ и пропускной способностью $$$|b_i|$$$.
- Для каждого $$$i$$$ такого, что $$$l \le i \le r$$$ и $$$b_i>0$$$, добавьте ребро от $$$i$$$ к $$$T$$$ со стоимостью $$$0$$$ и пропускной способностью $$$|b_i|$$$.
- Стоимость подмассива определяется как минимальная стоимость максимального потока из $$$S$$$ в $$$T$$$.
Вам даны $$$q$$$ запросов в виде двух целых чисел $$$l$$$ и $$$r$$$. Вы должны вычислить стоимость подмассива $$$a[l:r]$$$ для каждого запроса, по модулю $$$10^9 + 7$$$.
Если вы не знаете, что означает минимальная стоимость максимального потока, обратитесь сюда.
Первая строка ввода содержит два целых числа $$$n$$$ и $$$q$$$ $$$(2 \leq n \leq 2\cdot 10^5, 1 \leq q \leq 2\cdot10^5)$$$ — длину массивов $$$a$$$, $$$b$$$ и количество запросов.
Следующая строка содержит $$$n$$$ целых чисел $$$a_1,a_2 \ldots a_n$$$ ($$$0 \leq a_1 \le a_2 \ldots \le a_n \leq 10^9)$$$ — массив $$$a$$$. Гарантируется, что $$$a$$$ отсортирован в неубывающем порядке.
Следующая строка содержит $$$n$$$ целых чисел $$$b_1,b_2 \ldots b_n$$$ $$$(-10^9\leq b_i \leq 10^9, b_i \neq 0)$$$ — массив $$$b$$$.
В $$$i$$$-й из следующих $$$q$$$ строк содержится два целых числа $$$l_i,r_i$$$ $$$(1\leq l_i \leq r_i \leq n)$$$. Гарантируется, что $$$ \sum\limits_{j = l_i}^{r_i} b_j = 0$$$.
Для каждого запроса $$$l_i$$$, $$$r_i$$$ — выведите стоимость подмассива $$$a[l_i:r_i]$$$ по модулю $$$10^9 + 7$$$.
8 4 1 2 4 5 9 10 10 13 6 -1 1 -3 2 1 -1 1 2 3 6 7 3 5 2 6
2 0 9 15
В первом запросе, максимально возможный поток составляет $$$1$$$, т.е. одна единица из источника в $$$2$$$, затем одна единица из $$$2$$$ в $$$3$$$, затем одна единица из $$$3$$$ в сток. Стоимость потока равна $$$0 \cdot 1 + |2 - 4| \cdot 1 + 0 \cdot 1 = 2$$$.
Во втором запросе, максимально возможный поток снова составляет $$$1$$$, т.е. от источника к $$$7$$$, от $$$7$$$ к $$$6$$$ и от $$$6$$$ к стоку со стоимостью $$$0 \cdot |10 - 10| \cdot 1 + 0 \cdot 1 = 0$$$.
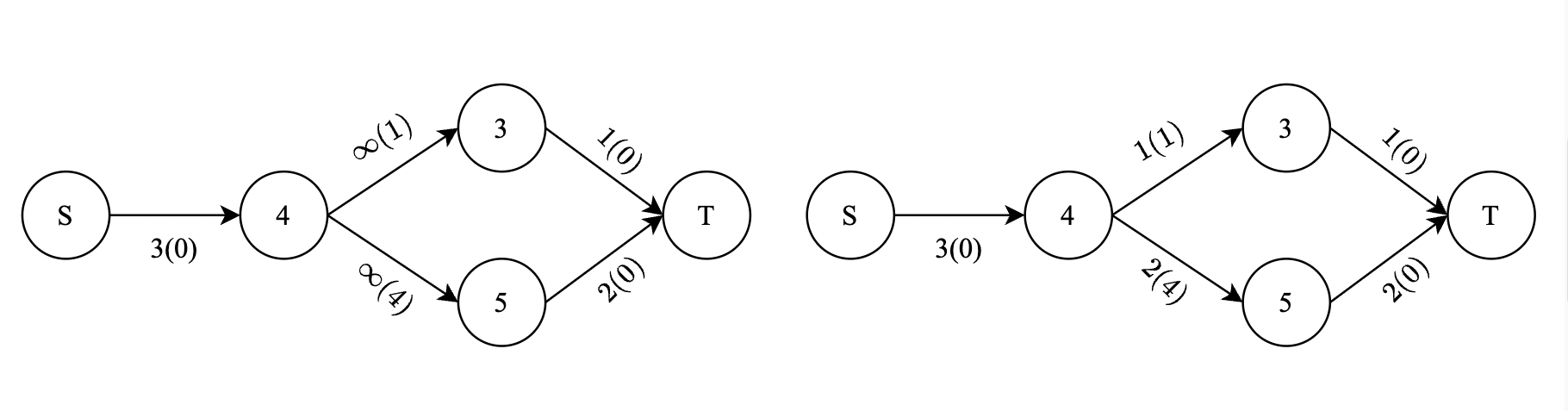
В третьем запросе, граф показан слева с пропускной способностью, указанной вне скобок, и стоимостью, указанной в скобках. Изображение справа показывает поток через каждое ребро в оптимальной конфигурации.
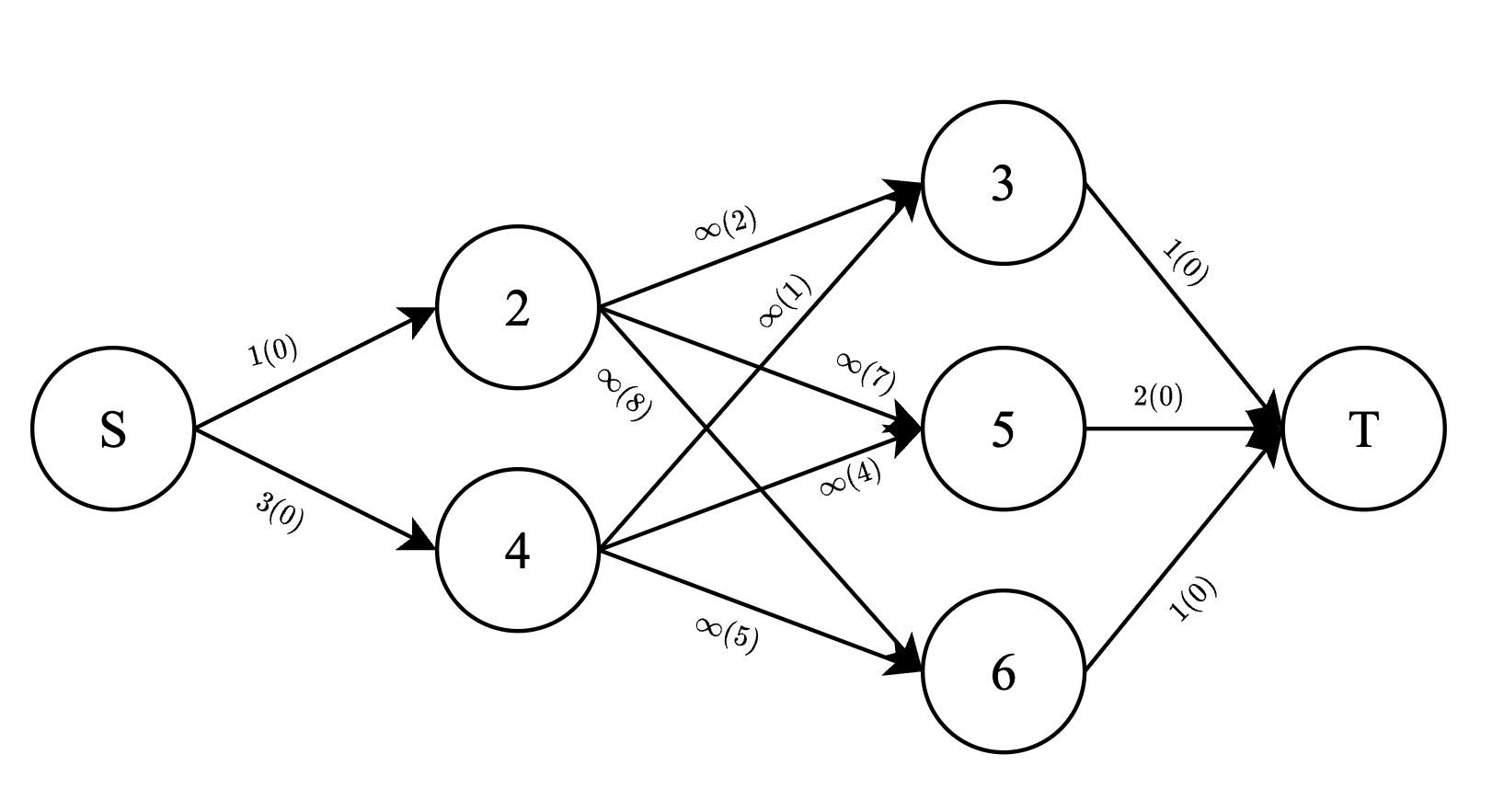
В четвертом запросе, сеть потока выглядит следующим образом:
Минимальная стоимость максимального потока достигается следующим образом:
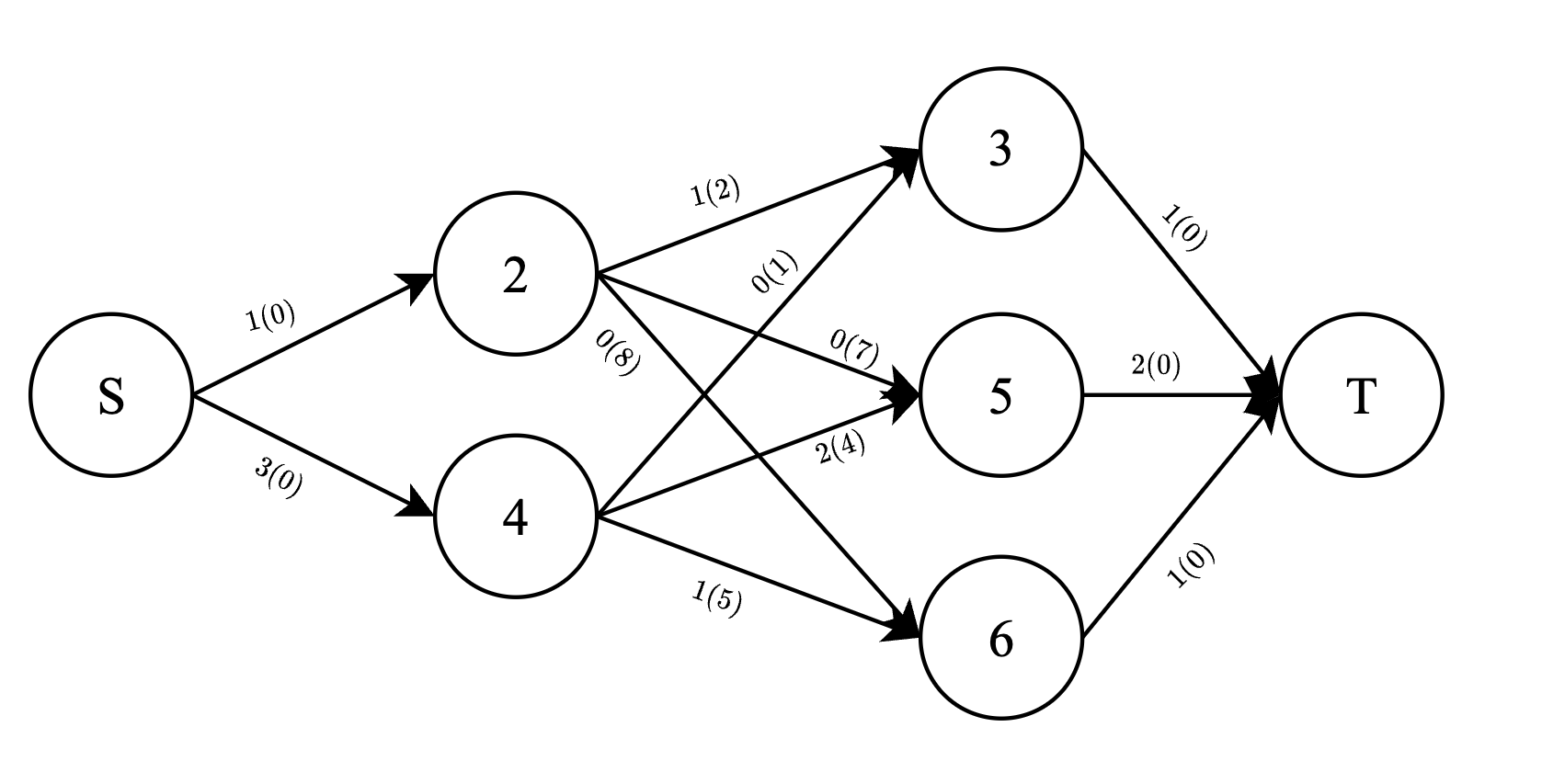
Максимальный поток в этой сети равен 4, а минимальная стоимость такого потока равна 15.
| Название |
|---|




