Вы нашли карту лабиринта довольно странной формы. Карта представляет собой сетку, разделенную на $$$n$$$ строк и $$$n$$$ столбцов. Строки карты пронумерованы от $$$1$$$ до $$$n$$$ снизу вверх. Столбцы карты пронумерованы от $$$1$$$ до $$$n$$$ слева направо.
В лабиринте есть $$$n$$$ слоев. Первый слой — это левый нижний угол (ячейка $$$(1, 1)$$$). Второй слой состоит из всех ячеек, которые внутри сетки и смежны с первым слоем по стороне или по углу. Третий слой состоит из всех ячеек, которые внутри сетки и смежны со вторым слоем по стороне или по углу.
Лабиринт из $$$5$$$ слоев, например, выглядит следующим образом:
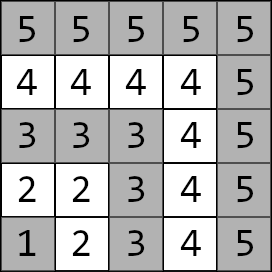
Слои отделены друг от друга стенами. Однако, в этих стенах есть двери.
В каждом слое (кроме слоя $$$n$$$) есть ровно две двери в следующий слой. Одна дверь размещена на верхней стене слоя, а другая дверь размещена на правой стене слоя. Для каждого слоя от $$$1$$$ до $$$n-1$$$ вам даны позиции этих двух дверей. Через эти двери можно ходить в обоих направлениях: либо из слоя $$$i$$$ в слой $$$i+1$$$, либо из слоя $$$i+1$$$ в слой $$$i$$$.
Если вы находитесь в какой-либо ячейке лабиринта, то вы можете переместиться в соседнюю по стороне клетку, если путь не преграждает стена (то есть нельзя переместиться в клетку в другом слое, если между клетками нет двери).
Вам нужно обработать $$$m$$$ запросов следующего вида: какое минимальное количество ходов необходимо сделать, чтобы дойти из клетки $$$(x_1, y_1)$$$ в клетку $$$(x_2, y_2)$$$?
В первой строке записано одно целое число $$$n$$$ ($$$2 \le n \le 10^5$$$) — количество слоев в лабиринте.
В $$$i$$$-й из следующих $$$n-1$$$ строк записаны четыре целых числа $$$d_{1,x}, d_{1,y}, d_{2,x}$$$ and $$$d_{2,y}$$$ ($$$1 \le d_{1,x}, d_{1,y}, d_{2,x}, d_{2,y} \le n$$$) — координаты дверей. Обе ячейки находятся на $$$i$$$-м слое. Первая ячейка смежна с верхней стеной $$$i$$$-го слоя по стороне — эта сторона — это место двери. Вторая ячейка смежна с правой стеной $$$i$$$-го слоя по стороне — эта сторона — это место двери.
В следующей строке записано одно целое число $$$m$$$ ($$$1 \le m \le 2 \cdot 10^5$$$) — количество запросов.
В $$$j$$$-й из следующих $$$m$$$ строк записаны четыре целых числа $$$x_1, y_1, x_2$$$ and $$$y_2$$$ ($$$1 \le x_1, y_1, x_2, y_2 \le n$$$) — координаты ячеек в $$$j$$$-м запросе.
На каждый запрос выведите одно целое число — минимальное количество ходов, которое необходимо сделать, чтобы дойти из клетки $$$(x_1, y_1)$$$ в клетку $$$(x_2, y_2)$$$.
2 1 1 1 1 10 1 1 1 1 1 1 1 2 1 1 2 1 1 1 2 2 1 2 1 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 2 2 2 2 2 2
0 1 1 2 0 2 1 0 1 0
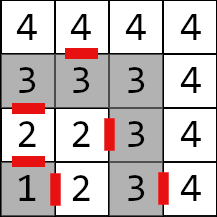
4 1 1 1 1 2 1 2 2 3 2 1 3 5 2 4 4 3 4 4 3 3 1 2 3 3 2 2 4 4 1 4 2 3
3 4 3 6 2
Здесь изображена карта лабиринта из второго примера. Двери отмечены красным.
| Название |
|---|




