Дан простой связный неориентированный граф, состоящий из $$$n$$$ вершин и $$$m$$$ ребер. Вершины пронумерованы от $$$1$$$ до $$$n$$$.
Вершинное покрытие графа — это такой набор вершин, что у каждого ребра есть хотя бы один конец в наборе.
Назовем свободным вершинным покрытием такое вершинное покрытие, что не более одного ребра имеет оба конца в наборе.
Найдите свободное вершинное покрытие графа или сообщите, что его нет. Если существует несколько ответов, то выведите любой из них.
В первой строке записано одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
В первой строке каждого набора входных данных записаны два целых числа $$$n$$$ и $$$m$$$ ($$$2 \le n \le 10^6$$$; $$$n - 1 \le m \le \min(10^6, \frac{n \cdot (n - 1)}{2})$$$) — количество вершин и количество ребер графа.
В каждой из следующих $$$m$$$ строк записаны два целых числа $$$v$$$ и $$$u$$$ ($$$1 \le v, u \le n$$$; $$$v \neq u$$$) — описания ребер.
В каждом наборе входных данных граф связный и не содержит кратных ребер. Сумма $$$n$$$ по всем наборам не превосходит $$$10^6$$$. Сумма $$$m$$$ по всем наборам не превосходит $$$10^6$$$.
На каждый набор входных данных в первой строке выведите YES, если свободное вершинное покрытие существует и NO, если нет. Если оно существует, то во второй строке выведите бинарную строку $$$s$$$ длины $$$n$$$, где $$$s_i = 1$$$ означает, что $$$i$$$-я вершина в вершинном покрытии, а $$$s_i = 0$$$ означает, что $$$i$$$-я вершина не в нем.
Если существует несколько ответов, то выведите любой из них.
46 51 32 43 43 54 64 61 22 33 41 41 32 48 111 32 43 54 65 76 81 23 45 67 87 24 51 22 33 41 32 4
YES 001100 NO YES 01100110 YES 0110
110 159 43 46 41 28 28 37 29 57 85 101 42 105 35 72 9
YES 0101100100
110 197 95 33 41 69 41 410 57 19 28 37 310 92 109 83 21 510 79 51 2
YES 1010000011
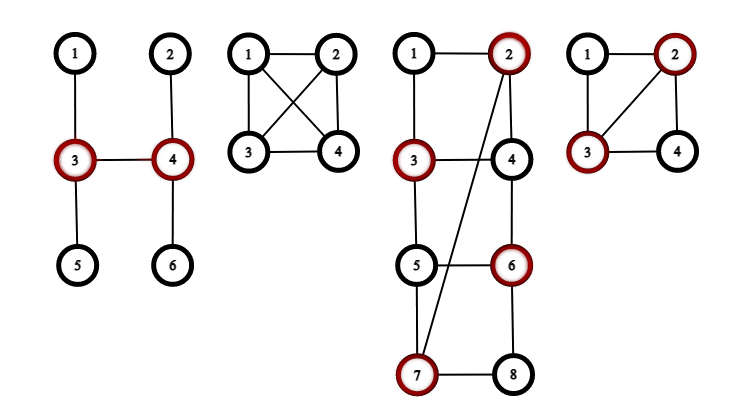
Здесь изображены графы из первого примера. Вершины в свободном вершинном покрытии помечены красным.
| Название |
|---|




