| Codeforces Round 791 (Div. 2) |
|---|
| Закончено |
У вас есть квадратная шахматная доска размера $$$n \times n$$$. Строки пронумерованы сверху вниз числами от $$$1$$$ до $$$n$$$, а столбцы — слева направо числами от $$$1$$$ до $$$n$$$. Таким образом, каждая клетка доски задается парой целых чисел $$$(x, y)$$$ ($$$1 \le x, y \le n$$$), где $$$x$$$ — номер строки, а $$$y$$$ — номер столбца.
От вас требуется выполнить $$$q$$$ запросов трех типов:
- Поставить новую ладью в клетку $$$(x, y)$$$.
- Убрать ладью из клетки $$$(x, y)$$$, куда ранее была поставлена ладья.
- Проверить, верно ли, что каждая клетка подпрямоугольника $$$(x_1, y_1) - (x_2, y_2)$$$ доски атакована хотя бы одной ладьей.
Подпрямоугольником называется множество клеток доски $$$(x, y)$$$, для которых верно, что $$$x_1 \le x \le x_2$$$ и $$$y_1 \le y \le y_2$$$.
Напомним, что клетка $$$(a, b)$$$ атакована ладьей, находящейся в клетке $$$(c, d)$$$, если $$$a = c$$$ или $$$b = d$$$. В частности, клетка, в которой находится ладья, атакована этой ладьей.
Первая строка содержит два целых числа $$$n$$$ и $$$q$$$ ($$$1 \le n \le 10^5$$$, $$$1 \le q \le 2 \cdot 10^5$$$) — размер доски и также количество запросов, соответственно.
Каждая из следующих $$$q$$$ строк содержит в себе описание очередного запроса. Описание запроса начинается с целого числа $$$t$$$ ($$$t \in \{1, 2, 3\}$$$), которое обозначает тип запроса:
- Если $$$t = 1$$$, далее следуют два целых числа $$$x$$$ и $$$y$$$ ($$$1 \le x, y \le n$$$) — координаты клетки, на которую нужно поставить новую ладью. Гарантируется, что в момент данного запроса в клетке $$$(x, y)$$$ не стоит ладья.
- Если $$$t = 2$$$, далее следуют два целых числа $$$x$$$ и $$$y$$$ ($$$1 \le x, y \le n$$$) — координаты клетки, с которой нужно убрать ладью. Гарантируется, что в момент данного запроса в клетке $$$(x, y)$$$ стоит ладья.
- Если $$$t = 3$$$, далее следуют четыре целых числа $$$x_1, y_1, x_2$$$ и $$$y_2$$$ ($$$1 \le x_1 \le x_2 \le n$$$, $$$1 \le y_1 \le y_2 \le n$$$) — подпрямоугольник, для которого нужно проверить, верно ли, что каждая его клетка атакована хотя бы одной ладьей.
Гарантируется, что среди $$$q$$$ запросов есть хотя бы один запрос третьего типа.
Для каждого запроса третьего типа в отдельной строке выведите «Yes» (без кавычек), если каждая клетка данного подпрямоугольника атакована хотя бы одной ладьей.
В противном случае выведите «No» (без кавычек).
8 10 1 2 4 3 6 2 7 2 1 3 2 3 6 2 7 2 1 4 3 3 2 6 4 8 2 4 3 3 2 6 4 8 1 4 8 3 2 6 4 8
No Yes Yes No Yes
Рассмотрим пример. После первых двух запросов доска будет выглядеть следующим образом (буквой $$$R$$$ обозначены клетки, в которых находится ладья, а зеленым выделен прямоугольник запроса третьего типа):

Доска после выполнения третьего и четвертого запросов:
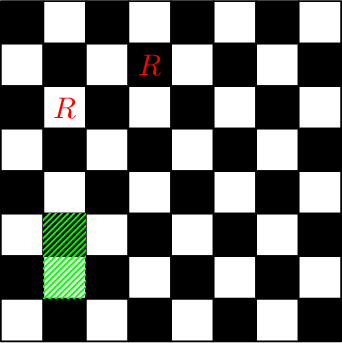
Доска после выполнения пятого и шестого запросов:
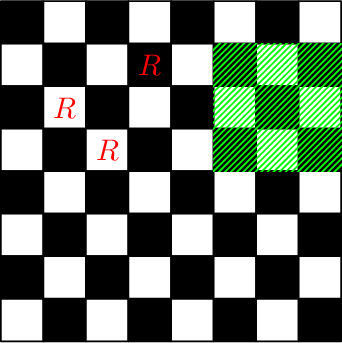
Доска после выполнения седьмого и восьмого запросов:
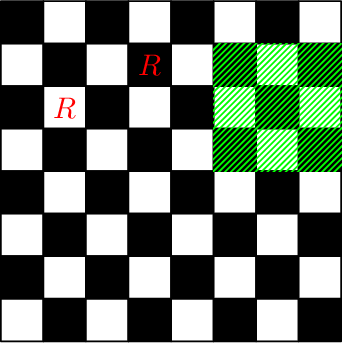
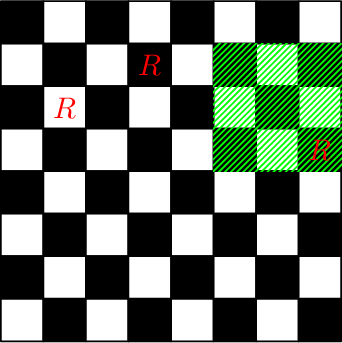
Доска после выполнения последних двух запросов:
| Название |
|---|




