| Codeforces Round 790 (Div. 4) |
|---|
| Закончено |
Вам дано подвешенное дерево из $$$n$$$ вершин, пронумерованных от $$$1$$$ до $$$n$$$. Корнем является вершина $$$1$$$. Также есть строка $$$s$$$, задающая цвета всех вершин: если $$$s_i = \texttt{B}$$$, то вершина $$$i$$$ чёрная, а если $$$s_i = \texttt{W}$$$, то вершина $$$i$$$ белая.
Поддерево дерева называется сбалансированным, если количество белых вершин поддерева равняется количеству чёрных вершин поддерева. Посчитайте количество сбалансированных поддеревьев.
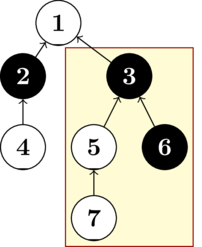 На картинке дерево при $$$n=7$$$, $$$a=[1,1,2,3,3,5]$$$ и $$$s=\texttt{WBBWWBW}$$$. Поддерево вершины $$$3$$$ сбалансированно.
На картинке дерево при $$$n=7$$$, $$$a=[1,1,2,3,3,5]$$$ и $$$s=\texttt{WBBWWBW}$$$. Поддерево вершины $$$3$$$ сбалансированно. Дерево — это связный граф без циклов. Подвешенное дерево — это дерево с выбранной вершиной, которую называют корнем. В этой задаче корнем каждого дерева является вершина $$$1$$$.
Дерево описано массивом предков $$$a_2, \dots, a_n$$$, содержащим $$$n-1$$$ число: $$$a_i$$$ — предок вершины с номером $$$i$$$ для всех $$$i = 2, \dots, n$$$. Предок вершины $$$u$$$ это следующая вершина на простом пути от $$$u$$$ к корню. Поддерево вершины $$$u$$$ — это множество всех вершин, которые содержат $$$u$$$ в пути к корню. Например на картинке выше, $$$7$$$ в поддереве у $$$3$$$, потому что простой путь $$$7 \to 5 \to 3 \to 1$$$ проходит через $$$3$$$. Обратите внимание, что сама вершина входит в своё поддерево, и поддеревом корня является всё дерево.
Первая строка входных данных содержит число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
Первая строка каждого набора содержит число $$$n$$$ ($$$2 \le n \le 4000$$$) — количество вершин в дереве.
Вторая строка каждого набора содержит $$$n-1$$$ число $$$a_2, \dots, a_n$$$ ($$$1 \le a_i < i$$$) — родители вершин $$$2, \dots, n$$$.
Третья строка каждого набора содержит строку $$$s$$$ длины $$$n$$$, состоящую из символов $$$\texttt{B}$$$ и $$$\texttt{W}$$$ — раскраска дерева.
Гарантируется, что сумма $$$n$$$ по всем наборам не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите одно число — количество сбалансированных поддеревьев.
3 7 1 1 2 3 3 5 WBBWWBW 2 1 BW 8 1 2 3 4 5 6 7 BWBWBWBW
2 1 4
Первый пример изображён в условии. Только поддеревья вершин $$$2$$$ и $$$3$$$ сбалансированны.
Во втором примере только поддерево вершины $$$1$$$ сбалансированно.
в третьем примере сбалансированны поддеревья вершин $$$1$$$, $$$3$$$, $$$5$$$ и $$$7$$$.
| Название |
|---|




