| Codeforces Round 785 (Div. 2) |
|---|
| Закончено |
Это интерактивная задача.
В городе есть $$$n^2$$$ зданий, разделенных на сетку из $$$n$$$ строк и $$$n$$$ столбцов. Вам нужно построить дорогу произвольной длины $$$D(A,B)$$$ между каждой парой соседних по стороне зданий $$$A$$$ и $$$B$$$. Из-за бюджетных и юридических ограничений длина каждой дороги должна быть положительным целым числом, а общая длина всех дорог не должна превышать $$$48\,000$$$.
В городе есть вор, который начнет с самого верхнего и самого левого здания (в первом ряду и первой колонке) и будет бродить по городу, время от времени крадя артефакты из некоторых зданий. Он может перемещаться из одного здания в другое соседнее здание, путешествуя по дороге, которая их соединяет.
Вы не можете отследить, какие здания он посещает и по какому пути он идет, чтобы добраться до них. Но в городе есть один следящий механизм. Трекер может хранить одно целое число $$$x$$$, которое изначально равно $$$0$$$. Каждый раз, когда вор перемещается из здания $$$A$$$ в соседнее здание $$$B$$$ по дороге длиной $$$D(A,B)$$$, трекер изменяет $$$x$$$ на $$$x\oplus D(A,B)$$$. Каждый раз, когда вор ворует из здания, трекер сообщает значение $$$x$$$, хранящееся в нем, и сбрасывает его обратно на $$$0$$$.
Заранее известно, что вор обворует ровно $$$k$$$ зданий, но значения, возвращаемые трекером, вы узнаете только после того, как кражи действительно произойдут. Ваша задача заключается в том, чтобы выбрать длины дорог таким образом, чтобы независимо от того, какой стратегии или маршрута придерживается вор, вы сможете точно сказать расположение всех зданий, где произошли кражи, по значениям, возвращаемым трекером.
Сначала считайте единственную строку, содержащую два целых числа $$$n$$$ $$$(2\leq n\leq 32)$$$ and $$$k$$$ $$$(1\leq k\leq 1024)$$$ — количество строк и количество краж соответственно.
Давайте обозначим $$$j$$$-е здание в $$$i$$$-й строке как $$$B_{i,j}$$$.
Затем выведите $$$n$$$ строк, каждая из которых содержит $$$n-1$$$ целое число. $$$j$$$-е число в $$$i$$$-й строке должно быть значением $$$D(B_{i,j},B_{i,j+1})$$$.
Затем выведите $$$n-1$$$ строку, каждая из которых содержит $$$n$$$ целых чисел. $$$j$$$-е число в $$$i$$$-й строке должно быть значением $$$D(B_{i,j},B_{i+1,j})$$$.
Помните, что суммарная длина дорог не должна превышать $$$48\,000$$$.
Затем ответьте на $$$k$$$ вопросов. Сначала считайте значение $$$x$$$, возвращаемое трекером. Потом выведите два целых числа, обозначающих номер строки и номер столбца здания, где произошла кража. После этого вы сможете ответить на следующий запрос (если такой есть).
После вывода запросов не забудьте вывести символ перевода строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы
Вы не можете делать взломы по этой задаче.
2 4 14 1 14 3
1 8 2 4 1 2 1 1 1 2 2 1
В примере $$$n=2$$$ and $$$k=4$$$.
Вы выбираете построить дороги следующих длин:
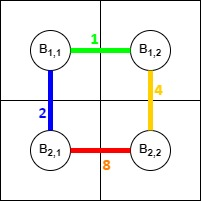
Вор действует следующим образом:
- Начать в $$$B_{1,1}$$$.
- Переместиться вправо в $$$B_{1,2}$$$.
- Переместиться вниз в $$$B_{2,2}$$$.
- Переместиться влево в $$$B_{2,1}$$$.
- Переместиться вверх в $$$B_{1,1}$$$.
- Переместиться вправо в $$$B_{1,2}$$$.
- Украсть из $$$B_{1,2}$$$.
- Переместиться влево в $$$B_{1,1}$$$.
- Украсть из $$$B_{1,1}$$$.
- Переместиться вниз в $$$B_{2,1}$$$.
- Переместиться вправо в $$$B_{2,2}$$$.
- Переместиться вверх в $$$B_{1,2}$$$.
- Украсть из $$$B_{1,2}$$$.
- Переместиться влево в $$$B_{1,1}$$$.
- Переместиться вниз в $$$B_{2,1}$$$.
- Украсть из $$$B_{2,1}$$$.
Трекер отвечает следующим образом:
- Изначально $$$x=0$$$.
- Изменить $$$x$$$ на $$$x\oplus 1=0\oplus1=1$$$.
- Изменить $$$x$$$ на $$$x\oplus 4=1\oplus4=5$$$.
- Изменить $$$x$$$ на $$$x\oplus 8=5\oplus8=13$$$.
- Изменить $$$x$$$ на $$$x\oplus 2=13\oplus2=15$$$.
- Изменить $$$x$$$ на $$$x\oplus 1=15\oplus1=14$$$.
- Вернуть $$$x=14$$$ и обнулить $$$x=0$$$.
- Изменить $$$x$$$ на $$$x\oplus 1=0\oplus1=1$$$.
- Вернуть $$$x=1$$$ и обнулить $$$x=0$$$.
- Изменить $$$x$$$ на $$$x\oplus 2=0\oplus2=2$$$.
- Изменить $$$x$$$ на $$$x\oplus 8=2\oplus8=10$$$.
- Изменить $$$x$$$ на $$$x\oplus 4=10\oplus4=14$$$.
- Вернуть $$$x=14$$$ и обнулить $$$x=0$$$.
- Изменить $$$x$$$ на $$$x\oplus 1=0\oplus1=1$$$.
- Изменить $$$x$$$ на $$$x\oplus 2=1\oplus2=3$$$.
- Вернуть $$$x=3$$$ и обнулить $$$x=0$$$.
| Название |
|---|




