| Codeforces Round 114 (Div. 1) |
|---|
| Закончено |
В некоторой стране живут волшебники. Они любят строить города и дороги.
Раньше в стране было k городов, j-ый (1 ≤ j ≤ k) был расположен в точке (xj, yj). Было решено наколдовать еще n - k городов. Причем i-ый (k < i ≤ n) город колдовался в точку с координатами (xi, yi):
- xi = (a·xi - 1 + b) mod (109 + 9)
- yi = (c·yi - 1 + d) mod (109 + 9)
Здесь a, b, c, d — простые числа. Причем a ≠ c, b ≠ d.
После постройки всех n городов, волшебники заметили удивительное свойство. Для любых двух различных городов с номерами i и j: xi ≠ xj и yi ≠ yj.
Города построены, пора строить дороги! Было решено использовать самое сложное (и, конечно же, самое мощное) заклинание для постройки дорог. C использованием этого заклинания, между городами u, v (yu > yv) проводится дорога тогда и только тогда, когда для любого города w, лежащего строго внутри уголка на точках u, v (см. ниже), есть город s, не лежащий в уголке, который находится по x-координате строго между w и u и при этом ys > yv.
Уголком на точках p2(x2, y2), p1(x1, y1) (y2 > y1) называется множество точек (x, y), для которых выполнено хотя бы одно из двух условий:
- min(x1, x2) ≤ x ≤ max(x1, x2) и y ≥ y1
- y1 ≤ y ≤ y2 и (x - x2)·(x1 - x2) ≥ 0
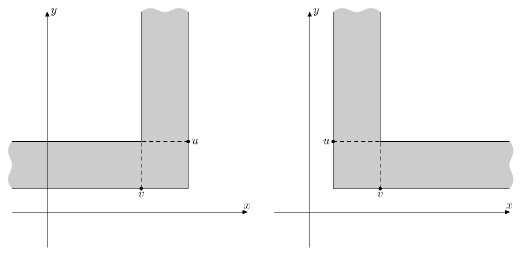 На рисунке изображены примеры уголков
На рисунке изображены примеры уголков Для того, чтобы опробовать заклинание, оно будет применено ко всем городам, лежащим по x-координате в отрезке [L, R]. После постройки дорог руководство страны хочет выбрать как можно больше пар городов, соединенных дорогой, так, что никакой город не лежит в двух или более парах. Вам предлагается для каждого из m предложенных вариантов выбора значений L, R посчитать максимальное количество таких пар после постройки дорог. Обратите внимание, что города, не лежащие в отрезке [L, R] по x-координате, никак не влияют на постройку дорог.
В первой строке через пробел записаны два целых числа n, k (1 ≤ k ≤ n ≤ 105, k ≤ 30). В следующих k строках записаны координаты точек расположения городов с первого по k-ый. В j-й строке записана через пробел пара целых чисел xj, yj (0 ≤ xj, yj < 109 + 9) — координаты j-го города.
В следующей строке через пробел записаны целые числа a, b, c, d (2 ≤ a, b, c, d < 109 + 9). Гарантируется, что эти числа простые, а так же, что a ≠ c, b ≠ d.
Гарантируется, что для любых двух различных городов с номерами i и j, xi ≠ xj и yi ≠ yj.
В следующей строке записано целое число m (1 ≤ m ≤ 105) — количество вариантов постройки дорог. В следующих m строках через пробел записаны пары целых чисел Li, Ri (0 ≤ Li ≤ Ri < 109 + 9) — варианты выбора городов, для постройки дорог.
Для каждой пары чисел Li, Ri выведите ответ на задачу в отдельной строке. Ответы для пар выводите в том порядке, в котором пары заданы во входных данных.
6 6
0 0
1 1
2 2
3 3
4 4
5 5
2 3 3 2
4
0 5
1 4
2 3
3 3
3
2
1
0
6 1
0 0
3 5 23917 11
4
0 1000000008
0 10
100 150
200 10000
2
1
0
1
В первом примере дороги соединяют города в цепочку в порядке возрастания x.
Во втором примере оставшиеся 5 городов будут построены в точках (5, 11); (20, 263098); (65, 292514823); (200, 76958738); (605, 622120197).
| Название |
|---|




