| Codeforces Round 780 (Div. 3) |
|---|
| Закончено |
Вам задана двоичная матрица $$$A$$$ размера $$$n \times n$$$. Строки пронумерованы сверху вниз от $$$1$$$ до $$$n$$$, столбцы пронумерованы слева направо от $$$1$$$ до $$$n$$$. Ячейка, находящаяся на пересечении строки $$$i$$$ и столбца $$$j$$$ называется $$$A_{ij}$$$. Рассмотрим набор из $$$4$$$ операций:
- Циклически сдвинуть все строки вверх. Строка с номером $$$i$$$ будет записана на место строки $$$i-1$$$ ($$$2 \le i \le n$$$), строка с номером $$$1$$$ будет записана на место строки $$$n$$$.
- Циклически сдвинуть все строки вниз. Строка с номером $$$i$$$ будет записана на место строки $$$i+1$$$ ($$$1 \le i \le n - 1$$$), строка с номером $$$n$$$ будет записана на место строки $$$1$$$.
- Циклически сдвинуть все столбцы влево. Столбец с номером $$$j$$$ будет записан на место столбца $$$j-1$$$ ($$$2 \le j \le n$$$), столбец с номером $$$1$$$ будет записан на место столбца $$$n$$$.
- Циклически сдвинуть все столбцы вправо. Столбец с номером $$$j$$$ будет записан на место столбца $$$j+1$$$ ($$$1 \le j \le n - 1$$$), столбец с номером $$$n$$$ будет записан на место столбца $$$1$$$.
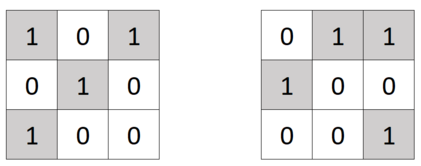 Слева изображена матрица $$$3 \times 3$$$ до применения к ней операции $$$3$$$, справа — после.
Слева изображена матрица $$$3 \times 3$$$ до применения к ней операции $$$3$$$, справа — после. Вы можете провести над матрицей произвольное (возможно, нулевое) количество операций, операции можно проводить в любом порядке.
После этого вы можете осуществить произвольное (возможно, нулевое) количество новых xor-операций:
- Выбрать любую ячейку $$$A_{ij}$$$ и записать в нее значение выражения $$$A_{ij} \oplus 1$$$. Другими словами, в ячейку $$$A_{ij}$$$ необходимо будет записать значение $$$(A_{ij} + 1) \bmod 2$$$.
Каждое применение этой xor-операции стоит один бурль. Заметим, что $$$4$$$ операции сдвигов — бесплатные. Эти $$$4$$$ операции можно проводить только до осуществления xor-операций.
Выведите минимальное количество бурлей, сколько придётся заплатить, чтобы сделать матрицу $$$A$$$ единичной. Единичной называется такая матрица, на главной диагонали которой стоят единицы, а остальные её элементы являются нулями (то есть, $$$A_{ij} = 1$$$ при $$$i = j$$$ и $$$A_{ij} = 0$$$ иначе).
В первой строке входных данных записано целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных в тесте.
Далее следуют описания наборов входных данных. Перед каждым набором входных данных во входных данных записана пустая строка.
В первой строке каждого набора входных данных записано единственное число $$$n$$$ ($$$1 \le n \le 2000$$$)
Затем следует $$$n$$$ строк, каждая из которых содержит ровно $$$n$$$ символов и состоит только из нулей и единиц. Эти строки описывают значения в ячейках матрицы.
Гарантируется, что сумма значений $$$n^2$$$ по всем наборам входных данных не превышает $$$4 \cdot 10^6$$$.
Для каждого набора входных данных выведите минимальное количество бурлей, сколько придётся заплатить, чтобы сделать матрицу $$$A$$$ единичной. Иными словами, выведите минимальное количество xor-операций, которое потребуется совершить после применения циклических сдвигов к матрице, для того, чтобы матрица $$$A$$$ стала единичной.
43010011100500010000011000001000001002101041111101111111111
1 0 2 11
В первом наборе входных данных можно действовать следующим образом: сначала циклически сдвинуть все строки вниз, тогда на главной диагонали матрицы будут стоять одни единицы. Затем необходимо будет применить xor-операцию к единственной единице, которая окажется не на главной диагонали.
Во втором наборе входных данных можно получить единичную матрицу, дважды применив к матрице операцию $$$2$$$ — циклический сдвиг строк вверх.
| Название |
|---|




