| Codeforces Round 782 (Div. 2) |
|---|
| Закончено |
Вам дан неориентированный связный граф из $$$n$$$ вершин и $$$m$$$ взвешенных ребер. Прогулкой от вершины $$$u$$$ до вершины $$$v$$$ называется последовательность вершин $$$p_1,p_2,\ldots,p_k$$$ (не обязательно различных), начинающаяся в вершине $$$u$$$ и заканчивающаяся в вершине $$$v$$$, такая что $$$p_i$$$ и $$$p_{i+1}$$$ соединены ребром для всех $$$1 \leq i < k$$$.
Определим длину прогулки следующим образом: выпишем веса ребер в порядке следования в массив. Затем выпишем побитовое И каждого непустого префикса этого массива. Длиной прогулки называется MEX этих значений.
Более формально, пусть веса ребер это $$$[w_1,w_2,\ldots,w_{k-1}]$$$, где $$$w_i$$$ — вес ребра между $$$p_i$$$ и $$$p_{i+1}$$$. Тогда длина прогулки равна $$$\mathrm{MEX}(\{w_1,\,w_1\& w_2,\,\ldots,\,w_1\& w_2\& \ldots\& w_{k-1}\})$$$, где $$$\&$$$ обозначает операцию побитового И.
Вы должны обработать $$$q$$$ запросов вида u v. Для каждого запроса найдите минимально возможную длину пути из $$$u$$$ в $$$v$$$.
MEX (минимальное отсутствующее) множества чисел — наименьшее неотрицательное число, отсутствующее в этом множестве. Например:
- MEX множества $$$\{2,1\}$$$ равен $$$0$$$, т. к. $$$0$$$ отсутствует в множестве.
- MEX множества $$$\{3,1,0\}$$$ равен $$$2$$$, т. к. $$$0$$$ и $$$1$$$ присутствуют в множестве, а $$$2$$$ — нет.
- MEX множества $$$\{0,3,1,2\}$$$ равен $$$4$$$, т. к. $$$0$$$, $$$1$$$, $$$2$$$ и $$$3$$$ присутствуют в множестве, а $$$4$$$ отсутствует.
Первая строка содержит два целых числа $$$n$$$ и $$$m$$$ ($$$2 \leq n \leq 10^5$$$; $$$n-1 \leq m \leq \min{\left(\frac{n(n-1)}{2},10^5\right)}$$$).
Каждая из следующих $$$m$$$ строк содержит три целых числа $$$a$$$, $$$b$$$ и $$$w$$$ ($$$1 \leq a, b \leq n$$$, $$$a \neq b$$$; $$$0 \leq w < 2^{30}$$$), обозначающих неориентированное ребро между вершинами $$$a$$$ и $$$b$$$ веса $$$w$$$. Гарантируется, что не существует петель и кратных ребер, а также что граф связный.
Следующая строка содержит одно целое число $$$q$$$ ($$$1 \leq q \leq 10^5$$$).
Каждая из следующих $$$q$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \leq u, v \leq n$$$, $$$u \neq v$$$) — описание запроса.
Для каждого запроса выведите одно целое число — ответ на запрос.
6 7 1 2 1 2 3 3 3 1 5 4 5 2 5 6 4 6 4 6 3 4 1 3 1 5 1 2 5 3
2 0 1
9 8 1 2 5 2 3 11 3 4 10 3 5 10 5 6 2 5 7 1 7 8 5 7 9 5 10 5 7 2 5 7 1 6 4 5 2 7 6 4 1 6 2 4 7 2 8
0 0 2 0 0 2 1 0 1 1
Ниже находится пояснение к первому примеру.
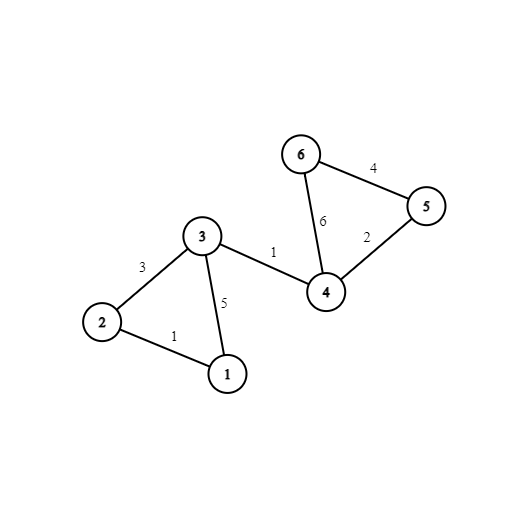 Граф из первого примера.
Граф из первого примера. Идна из возможных прогулок в первом запросе:
$$$$$$1 \overset{5}{\rightarrow} 3 \overset{3}{\rightarrow} 2 \overset{1}{\rightarrow} 1 \overset{5}{\rightarrow} 3 \overset{1}{\rightarrow} 4 \overset{2}{\rightarrow} 5.$$$$$$
Массив весов равен $$$w=[5,3,1,5,1,2]$$$. Если мы возьмем побитовое И для всех префиксов, мы получим множество $$$\{5,1,0\}$$$. MEX этого множества равен $$$2$$$. Нельзя получить прогулку меньшей длины.
| Название |
|---|




