| Codeforces Round 776 (Div. 3) |
|---|
| Закончено |
Сейчас у Дмитрия сессия, и он должен сдать $$$n$$$ экзаменов. Сессия начинается в день $$$1$$$ и длится $$$d$$$ дней. $$$i$$$-й экзамен пройдёт в день $$$a_i$$$ ($$$1 \le a_i \le d$$$), все $$$a_i$$$ — различны.
 Пример, где $$$n=3$$$, $$$d=12$$$, $$$a=[3,5,9]$$$. Оранжевым — дни сдачи экзамена. Перед первым экзаменом Дмитрий отдохнёт $$$2$$$ дня, перед вторым он отдохнёт $$$1$$$ день и перед третьим он отдохнёт $$$3$$$ дня.
Пример, где $$$n=3$$$, $$$d=12$$$, $$$a=[3,5,9]$$$. Оранжевым — дни сдачи экзамена. Перед первым экзаменом Дмитрий отдохнёт $$$2$$$ дня, перед вторым он отдохнёт $$$1$$$ день и перед третьим он отдохнёт $$$3$$$ дня. Для расписания сессии Дмитрий считает специальную величину $$$\mu$$$ — наименьшее из времен отдыха перед экзаменом по всем экзаменам. Например, для картинки выше $$$\mu=1$$$. Иными словами, для расписания он подсчитывает ровно $$$n$$$ чисел — сколько дней он отдыхает между экзаменом сдачей экзамена $$$i-1$$$ и $$$i$$$ (для $$$i=0$$$ между началом сессии и сдачей экзамена $$$i$$$). Затем он находит $$$\mu$$$ — минимум среди этих $$$n$$$ чисел.
Дмитрий считает, что может улучшить предложенное расписание сессии. Он может попросить изменить дату одного экзамена (изменить одно произвольное значение $$$a_i$$$). Помогите ему поменять дату так, чтобы все $$$a_i$$$ остались различны, а значение $$$\mu$$$ было как можно больше.
Например, для рассмотренного выше расписания Дмитрию наиболее выгодно перенести второй экзамен на самый конец сессии. Новое расписание примет вид:
 Теперь длительности отдыхов перед экзаменами равны $$$[2,2,5]$$$. Следовательно, $$$\mu=2$$$.
Теперь длительности отдыхов перед экзаменами равны $$$[2,2,5]$$$. Следовательно, $$$\mu=2$$$. Дмитрий может оставить предложенное расписание без изменений (если не существует способа передвинуть один экзамен так, что это приведёт к улучшению ситуации).
Первая строка входных данных содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следуют описания наборов входных данных.
Перед каждым набором в тесте записана пустая строка.
Первая строка описания каждого набора входных данных содержит два целых числа $$$n$$$ и $$$d$$$ ($$$2 \le n \le 2 \cdot 10^5, 1 \le d \le 10^9$$$) — количество экзаменов и длительность сессии, соответственно.
Вторая строка описания каждого набора входных данных содержит $$$n$$$ целых чисел $$$a_i$$$ ($$$1 \le a_i \le d, a_i < a_{i+1}$$$), где $$$i$$$-е число означает дату сдачи $$$i$$$-го экзамена.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите максимальное возможное значение $$$\mu$$$, если Дмитрий может перенести один любой экзамен на произвольный день. Все значения $$$a_i$$$ должны остаться различны.
93 123 5 92 51 52 1001 25 153 6 9 12 153 10000000001 400000000 5000000002 103 42 21 24 156 11 12 132 2017 20
2 1 1 2 99999999 3 0 1 9
Первый пример разобран в условии.
Одно из оптимальных изменений расписаний для второго примера:
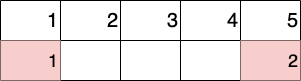 Изначальное расписание.
Изначальное расписание.
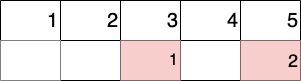 Новое расписание
Новое расписание
В третьем примере необходимо передвинуть экзамен с дня $$$1$$$ на любой день от $$$4$$$ до $$$100$$$.
В четвёртом примере любое изменение расписания только уменьшит $$$\mu$$$, соответственно расписание нужно оставить исходным.
В пятом примере необходимо перенести экзамен с дня $$$1$$$ на любой день от $$$100000000$$$ до $$$300000000$$$.
Одно из оптимальных изменений расписаний для шестого примера:
 Изначальное расписание.
Изначальное расписание.
 Новое расписание
Новое расписание
В седьмом примере каждый день занят экзаменами и перестроить расписание невозможно.
| Название |
|---|




