Задана сетка размера $$$n \times n$$$. Строки пронумерованы сверху вниз от $$$1$$$ до $$$n$$$, столбцы пронумерованы слева направо от $$$1$$$ до $$$n$$$.
Робот расположен в клетке $$$(1, 1)$$$. Он может делать два типа ходов:
- D — перейти на одну клетку вниз;
- R — перейти на одну клетку вправо.
Роботу запрещено выходить за пределы поля.
Дана последовательность ходов $$$s$$$ — изначальный маршрут робота. Этот маршрут не ведет робота за пределы поля.
Вам разрешено провести произвольное количество изменений строки (возможно, ноль). За одно изменение можно раздвоить один ход в последовательности. То есть, заменить одно вхождение D на DD или одно вхождение R на RR.
Посчитайте количество клеток таких, что существует хотя бы одна последовательность изменений, после применения которой робот посетит эту клетку на измененном маршруте и не выйдет за пределы поля.
В первой строке записано одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
В первой строке каждого набора записаны два целых числа $$$n$$$ ($$$2 \le n \le 10^8$$$) — количество строк и столбцов.
Во второй строке каждого набор записана непустая строка $$$s$$$, состоящая только из символов D и R, — изначальный маршрут робота. Этот маршрут не ведет робота за пределы поля.
Суммарная длина строк $$$s$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
На каждый набор входных данных выведите одно целое число — количество клеток таких, что существует хотя бы одна последовательность изменений, после применения которой робот посетит эту клетку на измененном маршруте и не выйдет за пределы поля.
34RD5DRDRDRDR3D
13 9 3
В первом наборе входных данных достаточно рассмотреть следующие измененные маршруты:
- RD $$$\rightarrow$$$ RRD $$$\rightarrow$$$ RRRD $$$\rightarrow$$$ RRRDD $$$\rightarrow$$$ RRRDDD — этот маршрут посещает клетки $$$(1, 1)$$$, $$$(1, 2)$$$, $$$(1, 3)$$$, $$$(1, 4)$$$, $$$(2, 4)$$$, $$$(3, 4)$$$ и $$$(4, 4)$$$;
- RD $$$\rightarrow$$$ RRD $$$\rightarrow$$$ RRDD $$$\rightarrow$$$ RRDDD — этот маршрут посещает клетки $$$(1, 1)$$$, $$$(1, 2)$$$, $$$(1, 3)$$$, $$$(2, 3)$$$, $$$(3, 3)$$$ и $$$(4, 3)$$$;
- RD $$$\rightarrow$$$ RDD $$$\rightarrow$$$ RDDD — этот маршрут посещает клетки $$$(1, 1)$$$, $$$(1, 2)$$$, $$$(2, 2)$$$, $$$(3, 2)$$$ и $$$(4, 2)$$$.
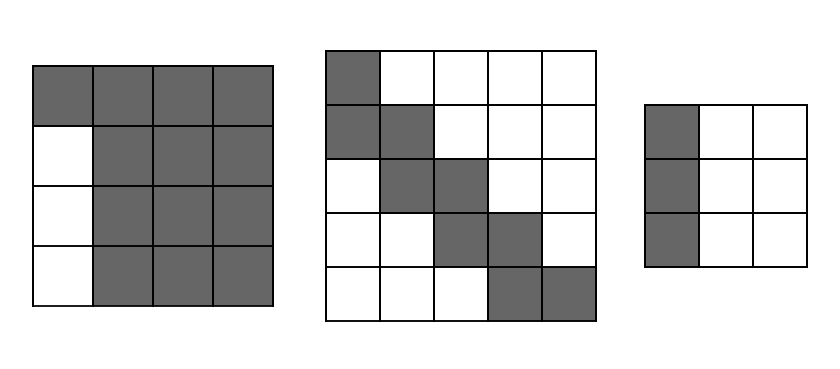
Таким образом, клетки, которые посещены на хотя бы одном измененном маршруте: $$$(1, 1)$$$, $$$(1, 2)$$$, $$$(1, 3)$$$, $$$(1, 4)$$$, $$$(2, 2)$$$, $$$(2, 3)$$$, $$$(2, 4)$$$, $$$(3, 2)$$$, $$$(3, 3)$$$, $$$(3, 4)$$$, $$$(4, 2)$$$, $$$(4, 3)$$$ и $$$(4, 4)$$$.
Во втором примере, нет способа изменить последовательность так, чтобы робот не вышел за пределы поля. Поэтому все посещенные клетки — это те, которые посещены на маршруте DRDRDRDR.
В третьем примере клетки, которые посещены на хотя бы одном измененном маршруте: $$$(1, 1)$$$, $$$(2, 1)$$$ и $$$(3, 1)$$$.
Клетки для всех наборов:
| Название |
|---|




