Задан связный взвешенный неориентированный граф, состоящий из $$$n$$$ вершин и $$$m$$$ ребер.
К нему задаются $$$k$$$ запросов. Каждый запрос состоит из одного целого числа $$$x$$$. На каждый запрос вы должны выбрать остовное дерево в графе. Пусть веса его ребер будут $$$w_1, w_2, \dots, w_{n-1}$$$. Стоимость остовного дерева равна $$$\sum \limits_{i=1}^{n-1} |w_i - x|$$$ (сумма абсолютных разностей между весами и $$$x$$$). Ответ на запрос — это минимальная стоимость остовного дерева.
Запросы даны в сжатом формате. Первые $$$p$$$ $$$(1 \le p \le k)$$$ запросов $$$q_1, q_2, \dots, q_p$$$ даны явно. Для запросов с $$$p+1$$$ по $$$k$$$ выполняется $$$q_j = (q_{j-1} \cdot a + b) \mod c$$$.
Выведите исключающее или ответов на все запросы.
В первой строке записаны два целых числа $$$n$$$ и $$$m$$$ ($$$2 \le n \le 50$$$; $$$n - 1 \le m \le 300$$$) — количество вершин и количество ребер в графе.
В каждой из следующих $$$m$$$ строк содержится описание неориентированного ребра: три целых числа $$$v$$$, $$$u$$$ и $$$w$$$ ($$$1 \le v, u \le n$$$; $$$v \neq u$$$; $$$0 \le w \le 10^8$$$) — вершины, которые соединяет ребро, и его вес. Обратите внимание, что между парой вершин может быть несколько ребер. Ребра образуют связный граф.
В следующей строке записаны пять целых чисел $$$p, k, a, b$$$ и $$$c$$$ ($$$1 \le p \le 10^5$$$; $$$p \le k \le 10^7$$$; $$$0 \le a, b \le 10^8$$$; $$$1 \le c \le 10^8$$$) — количество запросов, заданных явно, общее количество запросов и параметры для генерации запросов.
В следующей строке записаны $$$p$$$ целых чисел $$$q_1, q_2, \dots, q_p$$$ ($$$0 \le q_j < c$$$) — первые $$$p$$$ запросов.
Выведите одно целое число — исключающее или ответов на все запросы.
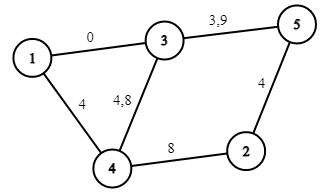
5 8 4 1 4 3 1 0 3 5 3 2 5 4 3 4 8 4 3 4 4 2 8 5 3 9 3 11 1 1 10 0 1 2
4
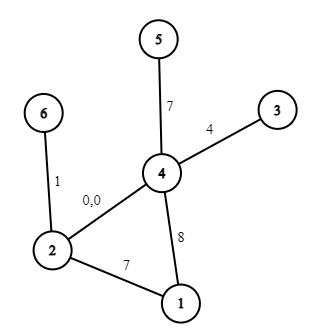
6 7 2 4 0 5 4 7 2 4 0 2 1 7 2 6 1 3 4 4 1 4 8 4 10 3 3 7 3 0 2 1
5
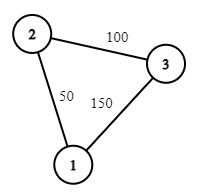
3 3 1 2 50 2 3 100 1 3 150 1 10000000 0 0 100000000 75
164
Запросы в первом примере: $$$0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0$$$. Ответы: $$$11, 9, 7, 3, 1, 5, 8, 7, 5, 7, 11$$$.
Запросы во втором примере: $$$3, 0, 2, 1, 6, 0, 3, 5, 4, 1$$$. Ответы: $$$14, 19, 15, 16, 11, 19, 14, 12, 13, 16$$$.
Запросы в третьем примере: $$$75, 0, 0, \dots$$$. Ответы: $$$50, 150, 150, \dots$$$.
| Название |
|---|




