E1. Дистанционное дерево (простая версия)
ограничение по времени на тест
2 секунды
ограничение по памяти на тест
512 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

Эта версия задачи отличается от следующей только ограничением на $$$n$$$.

Дерево — это связный неориентированный граф без циклов. Взвешенное дерево — это такое дерево, в котором у каждого ребра есть некоторый вес. Расстояние между вершинами — минимальная сумма весов на пути между ними.

Дано взвешенное дерево c $$$n$$$ вершинами, у каждого ребра вес $$$1$$$. Введём $$$d(v)$$$ как расстояние между вершиной $$$1$$$ и вершиной $$$v$$$.

Пусть $$$f(x)$$$ равно минимально возможному значению $$$\max\limits_{1 \leq v \leq n} \ {d(v)}$$$, если можно временно добавить одно ребро веса $$$x$$$ между любыми двумя вершинами $$$a$$$ и $$$b$$$ $$$(1 \le a, b \le n)$$$. Обратите внимание, что после этой операции граф уже не является деревом.

Для каждого целого числа $$$x$$$ от $$$1$$$ до $$$n$$$ найдите $$$f(x)$$$.

Входные данные

Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.

Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2 \le n \le 3000$$$).

Каждая из следующих $$$n−1$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u,v \le n$$$), указывающих на наличие ребра между вершинами $$$u$$$ и $$$v$$$. Гарантируется, что заданные ребра образуют дерево.

Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$3000$$$.

Выходные данные

Для каждого набора входных данных выведите в одной строке $$$n$$$ целых чисел, $$$x$$$-е из которых равно $$$f(x)$$$ для всех $$$x$$$ от $$$1$$$ до $$$n$$$.

Пример
Входные данные
3
4
1 2
2 3
1 4
2
1 2
7
1 2
1 3
3 4
3 5
3 6
5 7
Выходные данные
1 2 2 2 
1 1 
2 2 3 3 3 3 3
Примечание
В первом наборе входных данных:
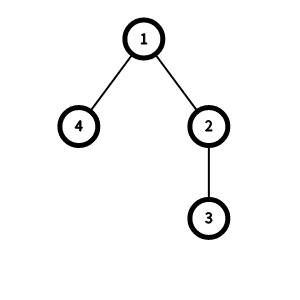
  • Для $$$x = 1$$$ мы можем добавить ребро между вершинами $$$1$$$ и $$$3$$$, после чего $$$d(1) = 0$$$ и $$$d(2) = d(3) = d(4) = 1$$$, поэтому $$$f(1) = 1$$$.
  • Для $$$x \ge 2$$$, вне зависимости от того, какое ребро мы добавим, $$$d(1) = 0$$$, $$$d(2) = d(4) = 1$$$ и $$$d(3) = 2$$$, поэтому $$$f(x) = 2$$$.