| Codeforces Round 768 (Div. 1) |
|---|
| Закончено |
Дан неориентированный граф, состоящий из $$$n$$$ вершин, пронумерованных от $$$1$$$ до $$$n$$$. Вершина $$$i$$$ имеет значение $$$a_i$$$, все $$$a_i$$$ попарно различны. Между вершинами $$$u$$$ и $$$v$$$ есть ребро, если либо $$$a_u$$$ делит $$$a_v$$$, либо $$$a_v$$$ делит $$$a_u$$$.
Найдите минимальное количество вершин, которое нужно удалить, чтобы граф стал двудольным. При удалении вершины удаляются все инцидентные ей ребра.
Каждый тест состоит из нескольких наборов входных данных. Первая строка каждого теста содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следует их описание.
Первая строка каждого набора содержит одно целое число $$$n$$$ ($$$1 \le n \le 5\cdot10^4$$$) — количество вершин в графе.
Вторая строка каждого набора содержит $$$n$$$ целых чисел, $$$i$$$-е число равно значению $$$a_i$$$ ($$$1 \le a_i \le 5\cdot10^4$$$) $$$i$$$-й вершины. Все $$$a_i$$$ различны.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$5\cdot10^4$$$.
Для каждого набора входных данных выведите одно число — минимальное количество вершин, которое нужно удалить, чтобы граф стал двудольным.
448 4 2 1430 2 3 5512 4 6 2 31085 195 5 39 3 13 266 154 14 2
2 0 1 2
В первом примере удалив вершины со значениями $$$1$$$ и $$$2$$$ мы получим двудольный граф. Таким образом ответ $$$2$$$. Невозможно удалить меньше $$$2$$$ вершин и получить двудольный граф.
| Before | After |
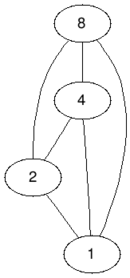 | 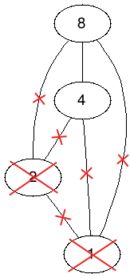 |
Во втором примере мы не должны удалять ни одну вершину, так как граф уже двудольный. Таким образом ответ $$$0$$$.
| Before | After |
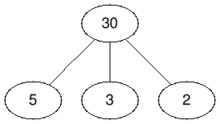 | 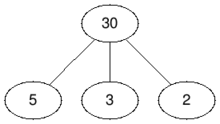 |
В третьем примере достаточно удалить вершину со значением $$$12$$$, таким образом ответ $$$1$$$.
| Before | After |
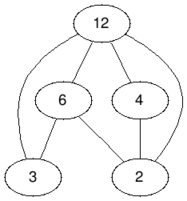 | 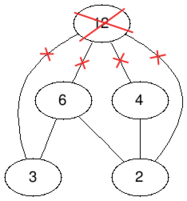 |
В четвертом примере мы удаляем вершины со значениями $$$2$$$ и $$$195$$$, значит ответ $$$2$$$.
| Before | After |
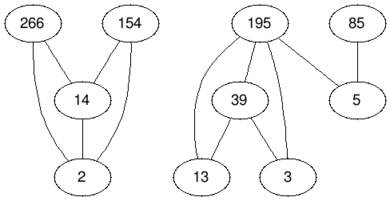 | 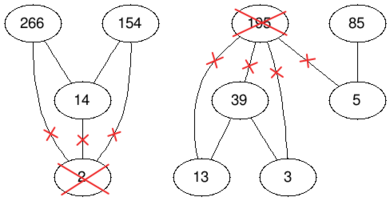 |
| Название |
|---|




