| VK Cup 2012 Раунд 2 |
|---|
| Закончено |
Как известно, лемминги любят прыгать. Для очередного эффектного группового прыжка n леммингов собрались у высокой скалы, на которой расположены k удобных уступов. Первый уступ расположен на высоте h метров, второй — на высоте 2h, и так далее (i-ый на высоте i·h метров). Лемминги собираются прыгать на закате, до которого осталось не так много времени.
Каждый лемминг характеризуется скоростью подъёма vi метров в минуту и массой mi. Это означает, что i-й лемминг может взобраться на j-й уступ за время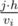 
минут.
Чтобы прыжок получился красивым, более тяжелые лемминги должны прыгать с более высоких уступов: если лемминг массой mi прыгает с уступа i, а лемминг массой mj прыгает с уступа j (для i < j), то должно выполняться неравенство mi ≤ mj.
Так как леммингов n, а уступов всего k (k ≤ n), то из n леммингов предстоит выбрать k, которые примут участие в прыжке. Выбранных леммингов нужно распределить по уступам с 1 по k по одному леммингу на уступ. Лемминги должны быть упорядочены в порядке неубывания массы с возрастанием высоты уступа. Кроме того, каждый лемминг должен успеть подняться на свой уступ, то есть время его подъёма не должно превышать t минут. Лемминги карабкаются на свои уступы все одновременно и не мешают друг другу.
Определите способ организовать прыжок леммингов таким образом, чтобы время t было минимально.
В первой строке через пробел заданы целые числа n, k и h (1 ≤ k ≤ n ≤ 105, 1 ≤ h ≤ 104) — общее количество леммингов, количество уступов и расстояние между соседними уступами.
Во второй строке через пробел записаны n целых чисел m1, m2, ..., mn (1 ≤ mi ≤ 109), где mi — масса i-го лемминга.
В третьей строке через пробел записаны n целых чисел v1, v2, ..., vn (1 ≤ vi ≤ 109), где vi — скорость i-го лемминга.
Выведите k различных чисел от 1 до n — номера леммингов, которые отправятся на уступы на высотах h, 2h, ..., kh, соответственно, при оптимальном способе организации прыжка. Если существует несколько способов выбрать леммингов, выведите любой.
5 3 2
1 2 3 2 1
1 2 1 2 10
5 2 4
5 3 10
3 4 3 2 1
5 4 3 2 1
4 3 1
Рассмотрим первый тестовый пример. Пятый лемминг со скоростью 10 забирается на уступ на высоте 2 за 
минуты; второй лемминг со скоростью 2 забирается на уступ на высоте 4 за 2 минуты; четвертый лемминг со скоростью 2 забирается на уступ на высоте 6 за 3 минуты. Все лемминги успевают занять свои места за 3 минуты.
