| Codeforces Round 767 (Div. 1) |
|---|
| Закончено |
NASA (Норвежская ассоциация астронавтов) разрабатывает новую систему управления космических кораблей. Но в нынешнем состоянии было бы небезопасно, если бы космический корабль оказался в кучке космического мусора. Чтобы система рулевого управления была безопасной, им необходимо ответить на следующее:
Для целевой позиции $$$t = (0, 0)$$$, набора из $$$n$$$ кусков космического мусора $$$l$$$, описанного отрезками $$$l_i = ((a_{ix}, a_{iy}), (b_{ix}, b_{iy}))$$$ и начальной позиции $$$s = (s_x, s_y)$$$, определите существует ли такое направление, что плавание в этом направлении из начальной позиции приведет к целевой позиции.
Когда космический корабль сталкивается с куском космического мусора, то, что происходит дальше, зависит от абсолютной разницы углов между направлением плавания и отрезком космического мусора, $$$\theta$$$:
- Если $$$\theta < 45^{\circ}$$$, то космический корабль скользит по куску космического мусора в направлении, минимизирующем изменение угла, а когда космический корабль оказывается на краю космического мусора, он продолжает двигаться в том же направлении как и до столкновения.
- Если $$$\theta \ge 45^{\circ}$$$, то космический корабль останавливается, потому что трение слишком велико, чтобы скользить по космическому мусору.
Вам дается набор кусочков космического мусора только один раз, целевая позиция всегда $$$(0, 0)$$$, но есть $$$q$$$ запросов, каждый с начальной позицией $$$s_j = (s_{jx}, s_{jy})$$$.
Ответьте на приведенный выше вопрос для каждого запроса.
В первой строке записано целое число $$$n$$$ ($$$1 \le n \le 1500$$$).
Далее следует $$$n$$$ строк, в $$$i$$$-й из которых содержатся $$$4$$$ целых числа $$$a_{ix}$$$, $$$a_{iy}$$$, $$$b_{ix}$$$ и $$$b_{iy}$$$ ($$$|a_{ix}|, |a_{iy}|, |b_{ix}|, |b_{iy}| \le 1000$$$).
Затем следует строка, содержащая целое число $$$q$$$ ($$$1 \le q \le 1000$$$).
Далее следует $$$q$$$ строк, $$$j$$$-я из которых содержит $$$2$$$ целых числа $$$s_{jx}$$$ и $$$s_{jy}$$$ ($$$|s_{jx}|, |s_{jy}| \le 1000$$$).
Гарантируется, что ни одна пара отрезков в наборе $$$l$$$ не пересекается и не соприкасается, $$$t$$$ не находится ни на одном отрезке из $$$l$$$, $$$s_j$$$ не находится ни на одном отрезке из $$$l$$$ и $$$s \neq t$$$.
На каждый запрос $$$s_j$$$ выведите ответ. Если существует такое направление, что плавание от $$$s_j$$$ в этом направлении, возможно, скользя по некоторым частям космического мусора, приводит к $$$t$$$, выведите «YES». В противном случае выведите «NO» (без учета регистра).
3 0 1 2 4 1 3 -1 6 0 -1 1 -1 14 -2 10 -1 10 0 10 1 10 2 10 3 10 4 10 5 10 6 10 -1 -2 0 -2 1 -2 2 -2 3 -2
YES YES YES YES YES NO NO NO YES YES NO NO NO YES
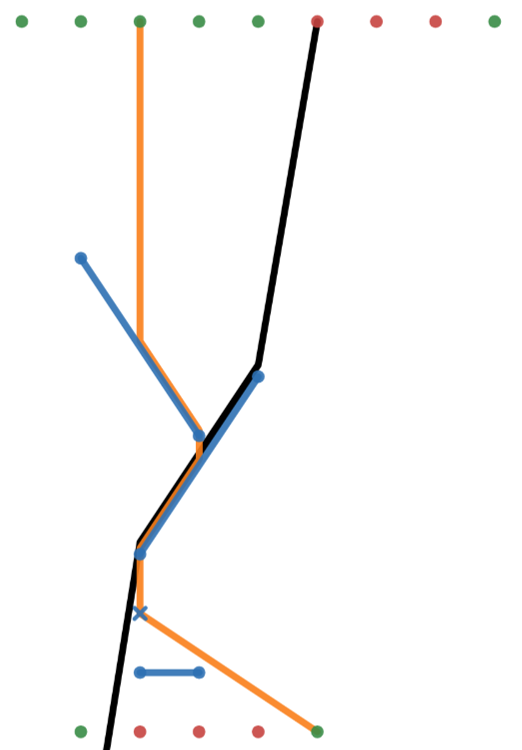
Синий крест представляет собой целевое местоположение, а другие отрезки синей линии представляют космический мусор.
Зеленые точки обозначают начальные местоположения, где ответ положительный, а красные точки обозначают начальные местоположения, где ответ отрицательный.
Желтые линии — это возможные пути к целевому местоположению для запросов $$$3$$$ и $$$14$$$.
Черная линия — это возможный путь от начального местоположения в запросе $$$6$$$, но он немного не попадает в целевое местоположение.
| Название |
|---|




