| Codeforces Round 767 (Div. 1) |
|---|
| Закончено |
Mihai живет в городе, где часто случаются метеоритные бури. Это раздражает, потому что Mihai иногда приходится покупать продукты, а попасть под метеориты крайне не весело. Поэтому мы просим вас найти самый опасный способ купить продукты, чтобы мы могли обманом заставить Mihai пойти туда.
В городе есть $$$n$$$ зданий с номерами от $$$1$$$ до $$$n$$$. Между некоторыми зданиями есть дороги, и существует ровно $$$1$$$ простой путь от любого здания к любому другому. Каждая дорога имеет определенный уровень метеоритной опасности. Во всех зданиях есть продуктовые магазины, но Mihai, конечно, интересуют только открытые магазины. Изначально все продуктовые магазины закрыты.
Вам задано $$$q$$$ запросов трех типов:
- Учитывая целые числа $$$l$$$ и $$$r$$$, в зданиях с номерами от $$$l$$$ до $$$r$$$ открываются продуктовые магазины (ничего не происходит со зданиями, в которых уже открыт продуктовый магазин).
- Учитывая целые числа $$$l$$$ и $$$r$$$, здания с номерами от $$$l$$$ до $$$r$$$ закрывают свои продуктовые магазины (ничего не происходит со зданиями, в которых уже закрыт продуктовый магазин).
- Учитывая целое число $$$x$$$, найдите максимальный уровень метеоритной опасности на простом пути от $$$x$$$ до любого открытого продуктового магазина или $$$-1$$$, если нет ни одной дороги на любом простом пути к любому открытому магазину.
В первой строке находятся два целых числа $$$n$$$ и $$$q$$$ ($$$2 \le n, q \le 3\cdot 10^5$$$).
Далее следует $$$n - 1$$$ строка, $$$i$$$-я из которых содержит целые числа $$$u_i$$$, $$$v_i$$$ и $$$w_i$$$ ($$$1 \le u_i, v_i \le n, \enspace 1 \le w_i \le 10^9$$$) — это означает, что между зданием $$$u_i$$$ и $$$v_i$$$ есть двусторонняя дорога с уровнем метеоритной опасности $$$w_i$$$.
Гарантируется, что данные ребра образуют дерево.
Далее следует $$$q$$$ строк, $$$j$$$-я из которых начинается с целого числа $$$t_j$$$ ($$$1 \le t_j \le 3$$$) и означает, что $$$j$$$-й запрос относится к типу $$$t_j$$$.
Если $$$t_j$$$ равно $$$1$$$ или $$$2$$$, то остальная часть строки содержит целые числа $$$l_j$$$ и $$$r_j$$$ ($$$1 \le l_j \le r_j \le n$$$).
Если $$$t_j$$$ равно $$$3$$$, то остальная часть строки содержит целое число $$$x_j$$$ ($$$1 \le x_j \le n$$$).
Для каждого запроса типа $$$3$$$ ($$$t_j = 3$$$) выведите максимальный уровень метеоритной опасности, который находится на некотором простом пути от $$$x_j$$$ до некоторого открытого магазина, или $$$-1$$$, если нет ни одной дороги на любом простом пути к любому открытому магазину.
6 9 1 3 1 2 3 2 4 5 3 4 6 4 3 4 5 3 1 1 1 1 3 1 2 1 1 1 5 6 3 4 2 6 6 3 4 3 1
-1 -1 4 3 5
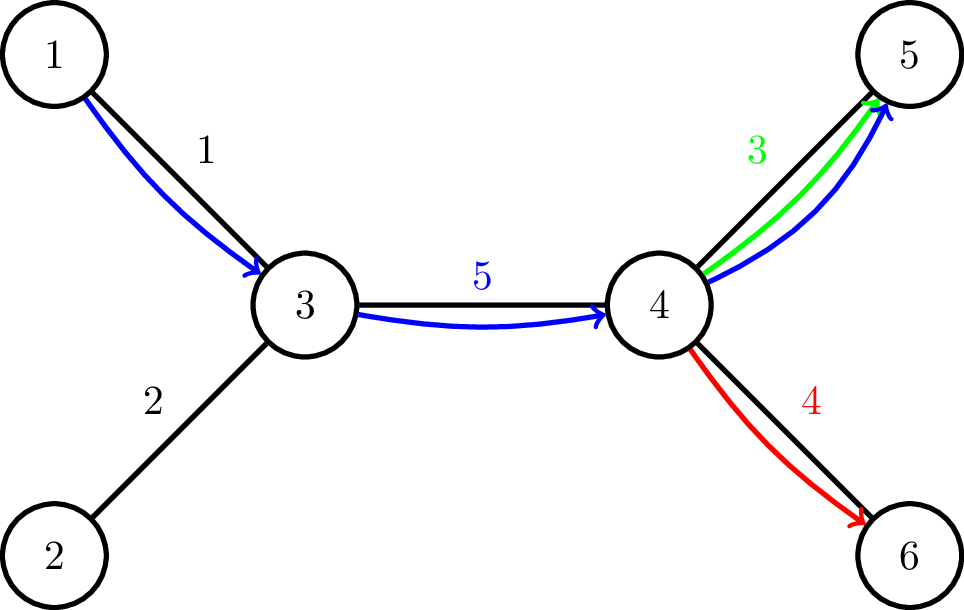
Это иллюстрация города, представленного во входных данных примера.
В первом запросе открытых магазинов нет, поэтому очевидно, что нет ребер на простом пути от $$$1$$$ до любого открытого магазина, поэтому ответ $$$-1$$$.
После второго и третьего запросов набор открытых магазинов равен $$$\{1\}$$$. Простой путь от $$$1$$$ до $$$1$$$ не имеет ребер, поэтому ответ для запроса $$$3$$$ равен $$$-1$$$.
После четвертого запроса открытых магазинов нет.
После пятого и шестого запросов набор открытых магазинов равен $$$\{5, 6\}$$$. В шестом запросе есть два пути от $$$x_j = 4$$$ до некоторого открытого продуктового магазина: От $$$4$$$ до $$$5$$$ и от $$$4$$$ до $$$6$$$. Самая большая метеоритная опасность находится на пути от $$$4$$$ до $$$6$$$, так что ответ на запрос $$$6$$$ будет $$$4$$$. На рисунке этот путь отмечен красным.
После остальных запросов набор открытых магазинов равен $$$\{5\}$$$.
В восьмом запросе единственный путь от $$$x_j = 4$$$ к открытому магазину от $$$4$$$ до $$$5$$$, а максимальная метеоритная опасность на этом пути составляет $$$3$$$. На рисунке этот путь отмечен зеленым.
В девятом запросе единственный путь от $$$x_j = 1$$$ к открытому магазину от $$$1$$$ до $$$5$$$, а максимальная метеоритная опасность на этом пути равна $$$5$$$. На рисунке этот путь отмечен синим цветом.
| Название |
|---|




