| Codeforces Round 766 (Div. 2) |
|---|
| Finished |
You are given a tree of $$$n$$$ vertices numbered from $$$1$$$ to $$$n$$$, with edges numbered from $$$1$$$ to $$$n-1$$$. A tree is a connected undirected graph without cycles. You have to assign integer weights to each edge of the tree, such that the resultant graph is a prime tree.
A prime tree is a tree where the weight of every path consisting of one or two edges is prime. A path should not visit any vertex twice. The weight of a path is the sum of edge weights on that path.
Consider the graph below. It is a prime tree as the weight of every path of two or less edges is prime. For example, the following path of two edges: $$$2 \to 1 \to 3$$$ has a weight of $$$11 + 2 = 13$$$, which is prime. Similarly, the path of one edge: $$$4 \to 3$$$ has a weight of $$$5$$$, which is also prime.
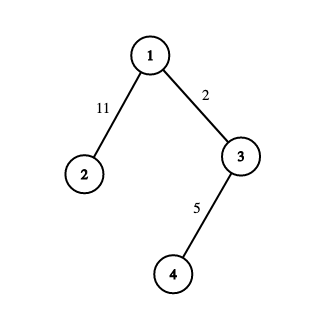
Print any valid assignment of weights such that the resultant tree is a prime tree. If there is no such assignment, then print $$$-1$$$. It can be proven that if a valid assignment exists, one exists with weights between $$$1$$$ and $$$10^5$$$ as well.
The input consists of multiple test cases. The first line contains an integer $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — the number of test cases. The description of the test cases follows.
The first line of each test case contains one integer $$$n$$$ ($$$2 \leq n \leq 10^5$$$) — the number of vertices in the tree.
Then, $$$n-1$$$ lines follow. The $$$i$$$-th line contains two integers $$$u$$$ and $$$v$$$ ($$$1 \leq u, v \leq n$$$) denoting that edge number $$$i$$$ is between vertices $$$u$$$ and $$$v$$$. It is guaranteed that the edges form a tree.
It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$10^5$$$.
For each test case, if a valid assignment exists, then print a single line containing $$$n-1$$$ integers $$$a_1, a_2, \dots, a_{n-1}$$$ ($$$1 \leq a_i \le 10^5$$$), where $$$a_i$$$ denotes the weight assigned to the edge numbered $$$i$$$. Otherwise, print $$$-1$$$.
If there are multiple solutions, you may print any.
3 2 1 2 4 1 3 4 3 2 1 7 1 2 1 3 3 4 3 5 6 2 7 2
17 2 5 11 -1
For the first test case, there are only two paths having one edge each: $$$1 \to 2$$$ and $$$2 \to 1$$$, both having a weight of $$$17$$$, which is prime.
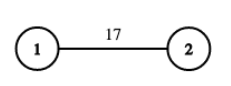
The second test case is described in the statement.
It can be proven that no such assignment exists for the third test case.
| Name |
|---|




