| Codeforces Round 766 (Div. 2) |
|---|
| Закончено |
Рахул и Тина с нетерпением ждут начала нового учебного года в колледже. Вот они заходят в учебный класс и видят, что места для студентов расположены в виде прямоугольника $$$n \times m$$$. Место, соответствующее клетке в строке $$$r$$$ столбце $$$c$$$ этого прямоугольника, обозначается как $$$(r, c)$$$. Расстояние между двумя местами $$$(a,b)$$$ и $$$(c,d)$$$ вычисляется по формуле $$$|a-c| + |b-d|$$$.
Как президент класса, Тина имеет доступ к ровно $$$k$$$ ведрам розовой краски. Далее происходит следующий процесс.
- Сначала Тина выбирает ровно $$$k$$$ мест в классе, чтобы покрасить их розовой краской. Одним ведром краски можно покрасить ровно одно место.
- После того как Тина покрасит $$$k$$$ мест в розовый цвет, Рахул выбирает, где ему сесть. Он не выберет место, покрашенное в розовый цвет, так как он очень не любит розовый.
- После того, как Рахул выберет свое место, Тина выбирает место для себя. Она может выбрать любое место, покрашенное или нет, за исключением того места, которое выбрал Рахул.
Рахул хочет выбрать место так, чтобы он сидел как можно ближе к Тине. Однако Тина хочет сидеть как можно дальше от Рахула из-за сложной истории отношений, которую мы решили не добавлять в условие задачи.
Теперь Рахул задается вопросом: для $$$k = 0, 1, \dots, n \cdot m - 1$$$, если у Тины есть $$$k$$$ ведер с краской, насколько близко Рахул может сидеть к Тине, если и Рахул, и Тина знают о намерениях друг друга и оба действуют оптимально? Пожалуйста, помогите удовлетворить любопытство Рахула!
Входные данные состоят из одного или нескольких наборов входных данных. Первая строка содержит целое число $$$t$$$ ($$$1 \leq t \leq 5 \cdot 10^4$$$) — количество наборов входных данных в тесте. Далее заданы описания наборов входных данных.
Единственная строка каждого набора входных данных содержит два целых числа $$$n$$$, $$$m$$$ ($$$2 \leq n \cdot m \leq 10^5$$$) — количество строк и столбцов в прямоугольнике, который описывает места студентов в классе.
Сумма значений $$$n \cdot m$$$ по всем наборам входных данных не превосходит $$$10^5$$$.
Для каждого набора входных данных выведите $$$n \cdot m$$$ целых чисел — расстояние между Рахулом и Тиной, если они оба действуют оптимально для каждого $$$k \in [0, n \cdot m - 1]$$$.
24 31 2
3 3 4 4 4 4 4 4 5 5 5 5 1 1
Одна из возможных последовательностей выбора для первого набора входных данных, где у Тины есть $$$k=3$$$ ведра с красками, выглядит следующим образом.
Тина красит места в позициях $$$(1, 2)$$$, $$$(2, 2)$$$, $$$(3, 2)$$$ розовой краской. Рахул выбирает место $$$(3, 1)$$$, после чего Тина выбирает место $$$(1, 3)$$$.
Следовательно, расстояние между Тиной и Рахулом равно $$$|3-1| + |1-3| = 4$$$. Мы можем доказать, что это действительно минимально возможное расстояние при заданных ограничениях. Могут быть и другие варианты мест, которые также приводят к тому же ответу.
При $$$k=0$$$ в первом наборе входных данных Рахул может решить сесть на $$$(2, 2)$$$, а Тина может сесть на $$$(4, 3)$$$, так что расстояние между ними будет $$$|2 - 4| + |2 - 3| = 3$$$.
Ниже приведены изображения случаев $$$k=3$$$ и $$$k=0$$$ для первого набора входных данных.
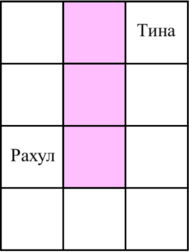 Возможная рассадка при $$$k=3$$$.
Возможная рассадка при $$$k=3$$$. 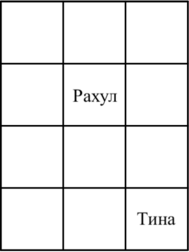 Возможная рассадка при $$$k=0$$$.
Возможная рассадка при $$$k=0$$$.
| Название |
|---|




