| Hello 2022 |
|---|
| Закончено |
Транспортная сеть одного крупного города состоит из $$$n$$$ станций, соединённых $$$n-1$$$ перегонами, и представляет собой дерево. Станция с номером $$$1$$$ является центром города. Для каждого перегона известно время в минутах, за которое его преодолевают поезда. Временем остановки поездов на станциях можно пренебречь. Обозначим за $$$dist(v)$$$ время, за которое можно доехать от станции $$$v$$$ до станции $$$1$$$.
Эта транспортная сеть разделена на зоны, для обозначения которых используются первые $$$k$$$ заглавных латинских букв. Зона станции $$$i$$$ обозначается как $$$z_i$$$. Центр города находится в зоне A. Для всех остальных станций выполнено, что ближайшая в направлении центра города станция находится в зоне с таким же, или лексикографически меньшим, обозначением. Любой перегон полностью принадлежит зоне его конца, более удалённого от центра города.
Турист летит в этот город на самолёте и по прибытии в аэропорт сразу направится в центр города. Опишем подробнее, как происходит поездка от станции $$$v$$$ до станции $$$1$$$:
- В момент времени $$$0$$$ турист садится на поезд, который едет от станции $$$v$$$ до станции $$$1$$$ по кратчайшему пути. Поездка займёт $$$dist(v)$$$ минут.
- В любой момент турист может купить билеты для любого подмножества зон. Билет для зоны $$$i$$$ стоит $$$pass_i$$$ евро.
- Каждые $$$T$$$ минут с момента посадки на поезд (то есть в моменты $$$T, 2T, \ldots$$$) его будет сканировать система контроля безбилетного проезда. Если туриста сканировали в зоне $$$i$$$ без билета для зоны $$$i$$$, он будет обязан заплатить штраф $$$fine_i$$$ евро. Зона в которой находится турист формально определяется следующим образом:
- Если турист находится на станции $$$1$$$, то он уже доехал до центра города и не должен платить штраф.
- Если турист находится на станции $$$u \neq 1$$$, то он находится в зоне $$$z_u$$$.
- Если турист едет по перегону от станции $$$x$$$ к станции $$$y$$$, то он находится в зоне $$$z_x$$$.
Турист всегда выберет такой способ оплаты проезда, который минимизирует количество потраченных евро. Для станции $$$v$$$ обозначим это число за $$$f(v)$$$.
К сожалению, турист не знает, чему равны текущие $$$pass_i$$$ и $$$fine_i$$$ для разных зон, а также не помнит, около какой станции находится аэропорт прибытия. Он будут делать разные предположения, а Вам предстоит обработать запросы $$$3$$$ видов:
- $$$1$$$ $$$i$$$ $$$c$$$ — запрос изменения стоимости билета в зоне $$$i$$$. Теперь $$$pass_i$$$ равно $$$c$$$.
- $$$2$$$ $$$i$$$ $$$c$$$ — запрос изменения штрафа в зоне $$$i$$$. Теперь $$$fine_i$$$ равно $$$c$$$.
- $$$3$$$ $$$u$$$ — решите следующую задачу для текущих значений $$$pass$$$ и $$$fine$$$:
- Дана станция $$$u$$$. Рассмотрим множество станций $$$v$$$, удовлетворяющих двум следующим условиям:
- $$$z_v = z_u$$$.
- Станция $$$u$$$ находится на пути от станции $$$v$$$ до станции $$$1$$$.
- Дана станция $$$u$$$. Рассмотрим множество станций $$$v$$$, удовлетворяющих двум следующим условиям:
В первой строке дано число $$$n$$$ ($$$2 \leq n \leq 2 \cdot 10^5$$$) — количество станций в транспортной сети.
Следующие $$$n - 1$$$ строка содержат по три числа $$$v_i$$$, $$$u_i$$$, $$$t_i$$$ ($$$1 \leq v_i, u_i \leq n, 1 \leq t_i \leq 10^9$$$) — концы $$$i$$$ перегона и время, за которое его преодолевают поезда. Гарантируется, что данные перегоны образуют дерево.
Следующая строка содержит число $$$k$$$ ($$$1 \leq k \leq 26$$$) — количество зон транспортной сети.
Следующая строка содержит $$$n$$$ символов $$$z_1z_2 \ldots z_n$$$ — где $$$z_i$$$ это обозначение зоны, в которой находится $$$i$$$ станция. Гарантируется, что условия из второго абзаца выполняются.
Следующая строка содержит $$$k$$$ чисел $$$pass_1$$$, $$$pass_2$$$, $$$\ldots$$$, $$$pass_k$$$ ($$$1 \leq pass_i \leq 10^9$$$) — изначальные стоимости билетов.
Следующая строка содержит $$$k$$$ чисел $$$fine_1$$$, $$$fine_2$$$, $$$\ldots$$$, $$$fine_k$$$ ($$$1 \leq fine_i \leq 10^9$$$) — изначальные размеры штрафов.
Следующая строка содержит число $$$T$$$ ($$$1 \leq T \leq 10^9$$$) — частоту сканирования туриста системой контроля безбилетного проезда.
Следующая строка содержит число $$$q$$$ ($$$1 \leq q \leq 2 \cdot 10^5$$$) — количество запросов.
Следующие $$$q$$$ строк содержат запросы в описанном в условии формате. Гарантируется, что в запросах первого и второго вида $$$i$$$ является корректным обозначением зоны (одной из первых $$$k$$$ заглавных латинских букв) и $$$1 \leq c \leq 10^9$$$, а в запросах третьего вида $$$1 \leq u \leq n$$$.
Для каждого запроса третьего вида выведите ответ на него в отдельной строке.
8 1 2 7 2 3 4 2 4 3 4 5 1 5 6 6 4 7 10 6 8 6 4 AABABBDB 11 12 10 42 16 15 15 30 4 6 3 2 1 A 10 3 3 2 A 3 3 7 3 6
0 10 6 6
Обратите внимание, что штраф может быть дешевле билета.
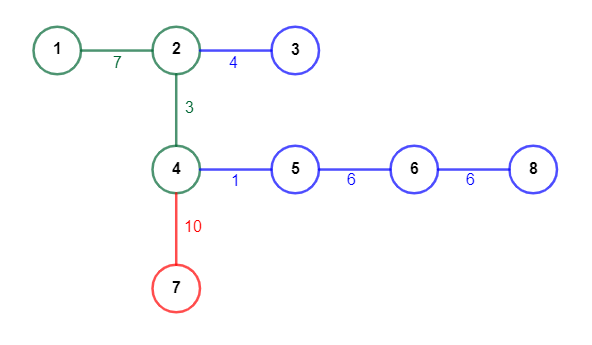Транспортная сеть из примера. Зелёным обозначены станции и перегоны, находящиеся в зоне A, синим — в зоне B, красным — в зоне D. Около каждого перегона указано время, за которое его преодолевают поезда. В первом запросе аэропорт может быть расположен около станции $$$2$$$ или около станции $$$4$$$. Во время поездки, турист всегда будет в зоне A. У него уже есть билет для этой зоны, поэтому ответ $$$0$$$.
После второго запроса стоимость билета в зоне A стала равна $$$10$$$.
В третьем запросе аэропорт может быть расположен только около станции $$$3$$$. Оптимальным решением будет купить билет для зоны A. В течении первых $$$3$$$ секунд поездки турист будет в зоне B. Потом он попадёт в зону A и будет сканирован там на $$$4$$$-й и $$$8$$$-й секундах поездки. Так как у него есть билет для этой зоны, он не будет платить штраф.
После четвёртого запроса штраф в зоне A стал равен $$$3$$$.
В пятом запросе аэропорт может быть расположен только около станции $$$7$$$ и $$$f(7) = 6$$$.
В шестом запросе аэропорт может быть расположен около станции $$$6$$$ или около станции $$$8$$$. Так как $$$f(6)=9$$$ и $$$f(8)=6$$$ ответ равен $$$6$$$.
