Дана матрица, состоящая из $$$n$$$ строк и $$$m$$$ столбцов. В $$$j$$$-й ячейке $$$i$$$-й строки записано целое число $$$a_{ij}$$$.
Сначала необходимо раскрасить каждую строку матрицы либо в красный, либо в синий цвет, так, чтобы хотя бы одна строка была красная и хотя бы одна строка была синяя.
Затем необходимо выбрать целое число $$$k$$$ ($$$1 \le k < m$$$) и разрезать матрицу таким образом, что первые $$$k$$$ столбцов становятся отдельной матрицей (левой матрицей) и последние $$$m-k$$$ столбцов становятся отдельной матрицей (правой матрицей).
Раскраска и разрез называются идеальными, если выполняются два условия:
- в каждой красной ячейке левой матрицы записано число большее, чем в каждой синей ячейке левой матрицы;
- в каждой синей ячейке правой матрицы записано число большее, чем в каждой красной ячейке правой матрицы.
Найдите любые идеальные раскраску и разрез или скажите, что таких нет.
В первой строке записано одно целое число $$$t$$$ ($$$1 \le t \le 1000$$$) — количество наборов входных данных.
Затем следуют описания $$$t$$$ наборов входных данных.
В первой строке каждого набора входных данных записаны два целых числа $$$n$$$ и $$$m$$$ ($$$2 \le n, m \le 5 \cdot 10^5$$$; $$$n \cdot m \le 10^6$$$) — количество строк и столбцов в матрице, соответственно.
В $$$i$$$-й из следующих $$$n$$$ строк записаны по $$$m$$$ целых чисел $$$a_{i1}, a_{i2}, \dots, a_{im}$$$ ($$$1 \le a_{ij} \le 10^6$$$).
Сумма $$$n \cdot m$$$ по всем наборам входных данных не превосходит $$$10^6$$$.
На каждый набор входных данных выведите ответ. Если нет идеальных раскраски и разреза, то выведите «NO».
Иначе, сначала выведите «YES». Затем строку, состоящую из $$$n$$$ символов: $$$i$$$-й символ должен быть 'R', если $$$i$$$-я строка покрашена в красный и 'B', если в синий. В строке должен быть хотя бы один символ 'R' и хотя бы один символ 'B'. Наконец, выведите целое число $$$k$$$ ($$$1 \le k < m$$$) — количество столбцов, которые отрезаются слева.
3 5 5 1 5 8 8 7 5 2 1 4 3 1 6 9 7 5 9 3 3 3 2 1 7 9 9 8 3 3 8 9 8 1 5 3 7 5 7 2 6 3 3 3 2 2 2 1 1 1 4 4 4
YES BRBRB 1 NO YES RB 3
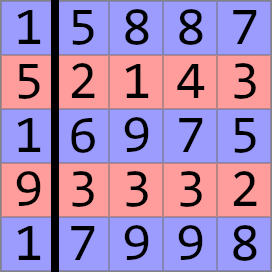
Раскраска и разрез для первого набора входных данных:
| Название |
|---|




