| Codeforces Round 754 (Div. 2) |
|---|
| Закончено |
Eikooc и Sushi играют в игру.
Игра проводится на дереве из $$$n$$$ вершин, пронумерованных от $$$1$$$ до $$$n$$$. Напомним, что дерево с $$$n$$$ вершинами это неориентированный связный граф с $$$n-1$$$ ребрами.
Игроки поочередно перемещают фишку по дереву. Eikooc делает первый ход, помещая фишку на любую вершину по своему выбору. Sushi делает следующий ход, затем Eikooc, затем Sushi, и так далее. В каждый ход после первого, игрок должен переместить фишку в какую-то вершину $$$u$$$ такую, что:
- Между вершинами $$$u$$$ и $$$v$$$ (на которой фишка находится данный момент), есть ребро
- $$$u$$$ не была посещена ранее
- $$$u \oplus v \leq min(u, v)$$$
Здесь $$$x \oplus y$$$ обозначает операцию побитового исключающего ИЛИ чисел $$$x$$$ и $$$y$$$.
Оба игрока играют оптимально. Игрок, который не может сделать ход, проигрывает.
Ниже приведены примеры, демонстрирующие правила игры.
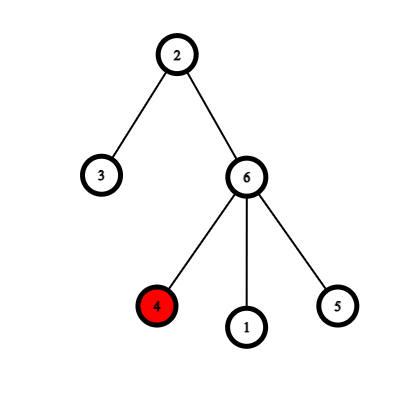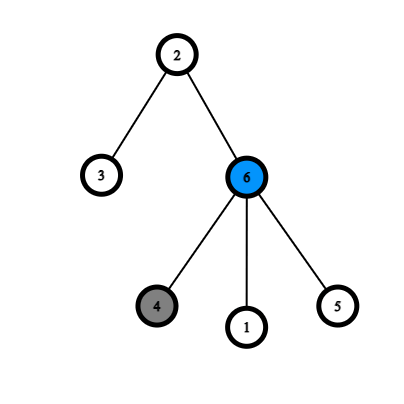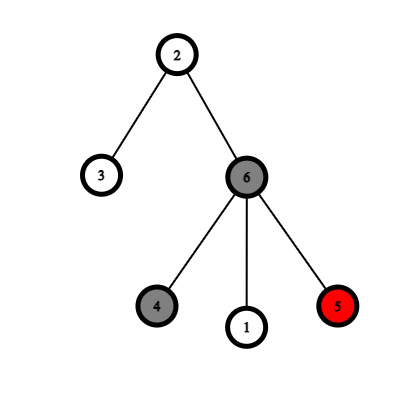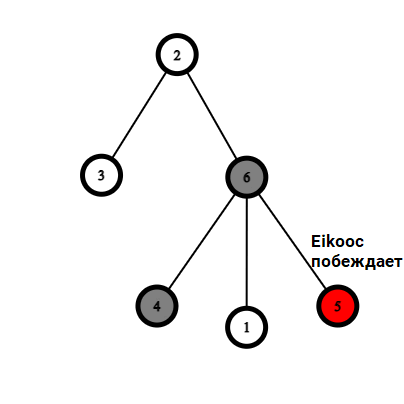 | 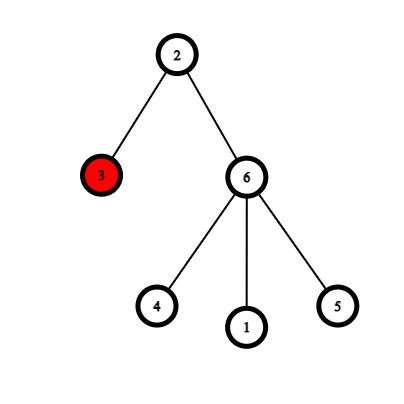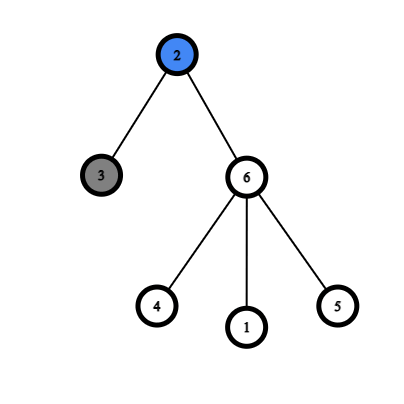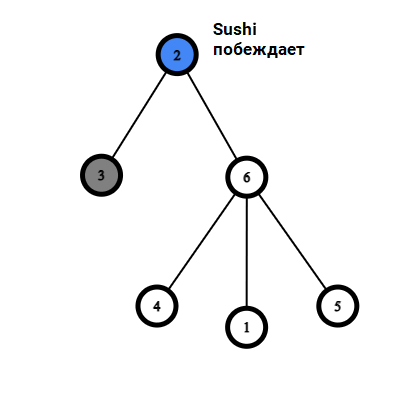 |
Перед началом игры Eikooc решает тайком перенумеровать вершины дерева в свою пользу. Формально, перенумерация — это перестановка $$$p$$$ длины $$$n$$$ (последовательность из $$$n$$$ целых чисел, где каждое целое число от $$$1$$$ до $$$n$$$ встречается ровно один раз), где $$$p_i$$$ обозначает новый номер вершины $$$i$$$.
Она хочет максимизировать количество вершин, которые она может выбрать в первый ход, для которых она сможет гарантировать себе победу. Помогите Eikooc найти любую перенумерацию, которая поможет ей в этом.
Первая строка содержит одно целое число $$$t~(1 \le t \le 10^5)$$$ — количество наборов входных данных. Описание каждого набора входных данных выглядит следующим образом.
Первая строка каждого набора входных данных содержит целое число $$$n~(1 \le n \le 2 \cdot 10^5)$$$ — количество вершин в дереве.
Следующие $$$n-1$$$ строки содержат по два целых числа $$$u$$$ и $$$v$$$ $$$(1 \le u, v \le n; u \neq v)$$$ — обозначающие ребро между вершинами $$$u$$$ и $$$v$$$.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите любую подходящую перестановку — перестановку длины $$$n$$$, которая максимизирует количество вершин, которые Eikooc может выбрать в первый ход и иметь выиграшную стратегию. Если таких перестановок несколько, вы можете вывести любую из них.
3 1 2 1 2 3 1 2 1 3
1 2 1 1 2 3
В первом наборе входных данных у Eikooc есть только одна вершина. У Sushi не будет ходов после того, как Eikooc выберет эту вершину, и Eikooc выиграет.
Во втором наборе входных данных $$$1 \oplus 2 = 3 \nleq min(1, 2)$$$. Следовательно, после того, как Eikooc выберет любую из вершин, у Sushi не останется ходов, и Eikooc выиграет. И $$$\{1, 2\}$$$, и $$$\{2, 1\}$$$ являются допустимыми перенумерациями.
| Название |
|---|




