| Codeforces Round 746 (Div. 2) |
|---|
| Закончено |
Это интерактивная задача!
На последнем региональном этапе Хемосе, ЗейадХаттаб и ЯхиаШериф — члены команды Carpe Diem — не прошли отбор на ICPC по каким-то неизвестным причинам. Хемосе был очень расстроен и у него был плохой день после соревнований, но ЗейадХаттаб очень мудрый и хорошо знает Хемосе, и не хочет видеть его грустным.
Зейад знает, что Хемосе любит задачи с деревьями, поэтому он дал ему задачу с деревом с очень особенным устройством.
У Хемоса есть взвешенное дерево на $$$n$$$ вершинах и $$$n-1$$$ ребрах. К сожалению, Хемосе не помнит веса ребер.
Определим $$$Dist(u, v)$$$ для $$$u\neq v$$$ как наибольший общий делитель весов всех ребер на пути от вершины $$$u$$$ к вершине $$$v$$$.
У Хемосе есть специальное устройство. Хемосе может дать устройству набор вершин, и устройство вернет наибольший $$$Dist$$$ между любыми двумя вершинами из этого набора. Более формально, если Хемосе даст устройству набор из $$$S$$$ узлов, устройство вернет наибольшее значение $$$Dist(u, v)$$$ по всем парам $$$(u, v)$$$, для которых $$$u$$$, $$$v$$$ $$$\in$$$ $$$S$$$ и $$$u \neq v$$$.
Хемосе может использовать это устройство не более $$$12$$$ раз, и хочет найти любые две различные вершины $$$a$$$, $$$b$$$ такие, что $$$Dist(a, b)$$$ является максимально возможным. Можете ли вы ему помочь?
Начните взаимодействие с чтения одного целого числа $$$n$$$ ($$$2 \le n \le 10^3$$$) — количества вершин в дереве.
Затем прочитайте $$$n-1$$$ строк.
$$$i$$$-я из следующих $$$n-1$$$ строк содержит два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \leq u_i, v_i \leq n$$$, $$$u_i\neq v_i$$$), что означает наличие ребра между вершинами $$$u_i$$$ и $$$v_i$$$.
Гарантируется, что веса ребер были $$$\leq 10^9$$$.
Гарантируется, что данный граф является деревом.
Теперь вы можете начать задавать запросы. Чтобы задать запрос о множестве из $$$k$$$ вершин $$$v_1, v_2, \ldots, v_k$$$ ($$$2 \le k \le n$$$, $$$1 \le v_i \le n$$$, все $$$v_i$$$ различны), выведите:
? $$$k$$$ $$$v_1$$$ $$$v_2$$$ $$$\ldots$$$ $$$v_k$$$.
Вы получите целое число $$$x$$$, наибольшее $$$Dist(v_i, v_j)$$$ по $$$1 \le i, j \le k$$$ с $$$i \neq j$$$.
Когда вы найдете $$$a$$$ и $$$b$$$ ($$$1 \le a, b \le n)$$$, $$$a\neq b$$$) такие, что $$$Dist(a, b)$$$ является максимально возможным, выведите ответ в следующем формате:
! $$$a$$$ $$$b$$$
Вывод ответа не учитывается в лимит в $$$12$$$ запросов.
Если существует несколько пар $$$(a, b)$$$ с одинаковым наибольшим $$$Dist(a, b)$$$, можно вывести любую.
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы
Чтобы взломать решение, используйте следующий формат.
Первая строка должна содержать одно целое число $$$n$$$ $$$(2 \leq n \le 10^3)$$$ — количество вершин.
В $$$i$$$-й из следующих $$$n-1$$$ строк должно содержаться три целых числа $$$u_i$$$, $$$v_i$$$, $$$w_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i\ne v_i$$$, $$$1 \le w \le 10^9$$$), что означает, что между вершинами $$$u_i$$$ и $$$v_i$$$ есть ребро с весом $$$w_i$$$.
Эти $$$n-1$$$ ребер должны образовывать дерево.
6 1 2 2 3 2 4 1 5 5 6 10 2 10
? 6 1 2 3 4 5 6 ? 3 3 1 5 ? 2 1 2 ! 1 2
Дерево в первом примере приведено ниже:
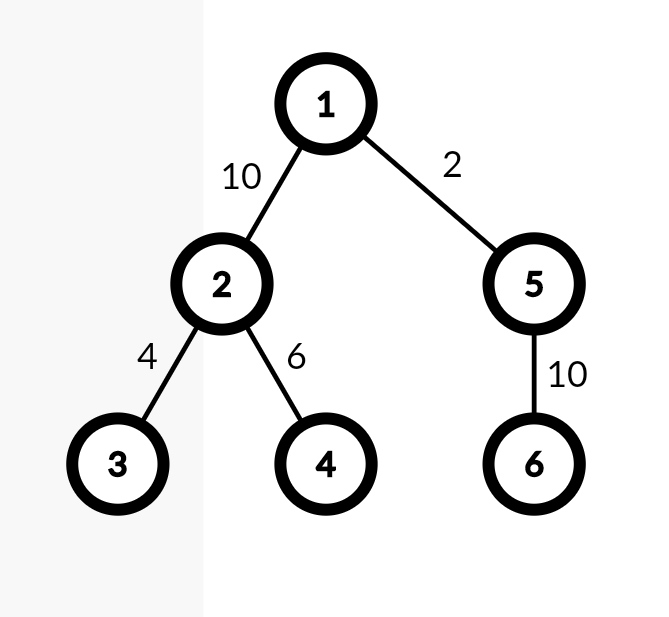
| Название |
|---|




