| Технокубок 2022 - Отборочный Раунд 1 |
|---|
| Закончено |
Она делает все возможное, чтобы безупречно провести последний обряд человека и сохранить баланс инь и ян в мире.
Ху Тао, будучи маленькой проказницей, попыталась напугать вас этой задачей с графом! Вам дан связный неориентированный граф из $$$n$$$ вершин с $$$m$$$ ребрами. У вас также есть $$$q$$$ запросов. Каждый запрос состоит из двух вершин $$$a$$$ и $$$b$$$.
Изначально все ребра графа имеют вес $$$0$$$. Для каждого запроса вы должны выбрать простой путь, начинающийся из $$$a$$$ и заканчивающийся в $$$b$$$. Затем к весу каждого ребра вдоль этого пути добавляется $$$1$$$. Определите, возможно ли, чтобы после обработки всех $$$q$$$ запросов все ребра в этом графе имели четный вес. Если да, то выведите выбор путей для каждого запроса.
Если это невозможно, определите наименьшее количество дополнительных запросов, которые можно добавить, чтобы это стало возможным. Можно показать, что при заданных ограничениях это число не превысит $$$10^{18}$$$.
Простой путь определяется как любой путь, который не посещает вершину более одного раза.
Считается, что ребро имеет четный вес, если его значение кратно $$$2$$$.
Первая строка содержит два целых числа $$$n$$$ и $$$m$$$ ($$$2 \leq n \leq 3 \cdot 10^5$$$, $$$n-1 \leq m \leq \min{\left(\frac{n(n-1)}{2}, 3 \cdot 10^5\right)}$$$).
Каждая из следующих $$$m$$$ строк содержит два целых числа $$$x$$$ и $$$y$$$ ($$$1 \leq x, y \leq n$$$, $$$x\neq y$$$), указывающих на неориентированное ребро между вершинами $$$x$$$ и $$$y$$$. Входные данные не будут содержать петель или дублирующихся ребер, и полученный граф будет связным.
Следующая строка содержит одно целое число $$$q$$$ ($$$1 \leq q \leq 3 \cdot 10^5$$$).
Каждая из следующих $$$q$$$ строк содержит два целых числа $$$a$$$ и $$$b$$$ ($$$1 \leq a, b \leq n, a \neq b$$$), описание каждого запроса.
Гарантируется, что $$$nq \leq 3 \cdot 10^5$$$.
Если можно заставить все веса ребер быть четными, выведите «YES» в первой строке, а затем $$$2q$$$ строк, указывающих выбор пути для каждого запроса в том же порядке, в котором задаются запросы. Для каждого запроса первая строка должна содержать одно целое число $$$x$$$: количество узлов в выбранном пути. Следующая строка должна содержать $$$x$$$ целых чисел $$$p_i$$$, указывающих выбранный путь ($$$p_1 = a, p_x = b$$$ и все числа должны лежать между $$$1$$$ и $$$n$$$). Этот путь не может содержать одну вершину более одного раза и должен быть корректным простым путем в графе.
Если невозможно заставить все веса ребер быть четными, выведите «NO» в первой строке и минимальное количество запросов, которые нужно добавить, во второй строке.
6 7 2 1 2 3 3 5 1 4 6 1 5 6 4 5 3 1 4 5 1 4 5
YES 2 1 4 4 5 3 2 1 5 4 1 2 3 5
5 7 4 3 4 5 2 1 1 4 1 3 3 5 3 2 4 4 2 3 5 5 1 4 5
NO 2
Вот как выглядят запросы для первого примера (красный цвет соответствует 1-му запросу, синий — 2-му, а зеленый — 3-му):
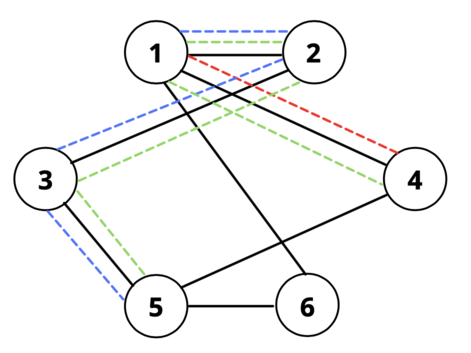
Граф во втором примере выглядит следующим образом:
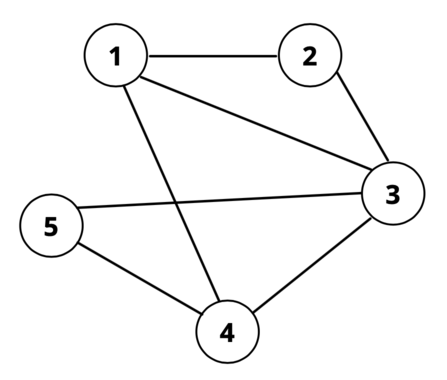
| Название |
|---|




