Mr. Chanek's city can be represented as a plane. He wants to build a housing complex in the city.
There are some telephone poles on the plane, which is represented by a grid $$$a$$$ of size $$$(n + 1) \times (m + 1)$$$. There is a telephone pole at $$$(x, y)$$$ if $$$a_{x, y} = 1$$$.
For each point $$$(x, y)$$$, define $$$S(x, y)$$$ as the square of the Euclidean distance between the nearest pole and $$$(x, y)$$$. Formally, the square of the Euclidean distance between two points $$$(x_1, y_1)$$$ and $$$(x_2, y_2)$$$ is $$$(x_2 - x_1)^2 + (y_2 - y_1)^2$$$.
To optimize the building plan, the project supervisor asks you the sum of all $$$S(x, y)$$$ for each $$$0 \leq x \leq n$$$ and $$$0 \leq y \leq m$$$. Help him by finding the value of $$$\sum_{x=0}^{n} {\sum_{y=0}^{m} {S(x, y)}}$$$.
The first line contains two integers $$$n$$$ and $$$m$$$ ($$$0 \leq n, m < 2000$$$) — the size of the grid.
Then $$$(n + 1)$$$ lines follow, each containing $$$(m + 1)$$$ integers $$$a_{i, j}$$$ ($$$0 \leq a_{i, j} \leq 1$$$) — the grid denoting the positions of telephone poles in the plane. There is at least one telephone pole in the given grid.
Output an integer denoting the value of $$$\sum_{x=0}^{n} {\sum_{y=0}^{m} {S(x, y)}}$$$.
2 2 101 000 000
18
5 4 10010 00000 01000 00001 00100 00010
36
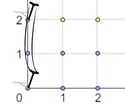
In the first example, the nearest telephone pole for the points $$$(0,0)$$$, $$$(1,0)$$$, $$$(2,0)$$$, $$$(0,1)$$$, $$$(1,1)$$$, and $$$(2,1)$$$ is at $$$(0, 0)$$$. While the nearest telephone pole for the points $$$(0, 2)$$$, $$$(1,2)$$$, and $$$(2,2)$$$ is at $$$(0, 2)$$$. Thus, $$$\sum_{x=0}^{n} {\sum_{y=0}^{m} {S(x, y)}} = (0 + 1 + 4) + (1 + 2 + 5) + (0 + 1 + 4) = 18$$$.
| Name |
|---|




