| Kotlin Heroes: Episode 8 |
|---|
| Закончено |
- Kotlin 1.7.20
- Kotlin 1.9.21
Ира разрабатывает компьютерную игру. В данной игре есть рандомизированные генерация и сложность уровней. Для достижения случайной сложности, некоторые противники на уровне случайным образом заменяются на более сильных.
Для того чтобы описать уровни в игре, введем координатную плоскость так, чтобы ось $$$Ox$$$ была направлена слева направо, а ось $$$Oy$$$ — снизу вверх. Уровень — это прямоугольник с противоположными углами в точках $$$(0, 0)$$$ и $$$(a, b)$$$. Позиция каждого противника на уровне — это точка в прямоугольнике.
На данный момент Ира реализовала противников только одного типа в двух версиях — базовом и усиленном. Обе версии противников стреляют лазерными лучами в нескольких направлениях:
- базовые противники стреляют лазером в четыре направления: вправо (в направлении вектора $$$(1, 0)$$$), влево (в направлении вектора $$$(-1, 0)$$$), вверх (в направлении вектора $$$(0, 1)$$$) и вниз (в направлении вектора $$$(0, -1)$$$);
- усиленные противника стреляют лазеров в восемь направлений: четыре направления совпадают с базовой версией, а еще четыре — в направление векторов $$$(1, 1)$$$, $$$(1, -1)$$$, $$$(-1, 1)$$$, $$$(-1, -1)$$$.
Лучи лазеров проходят сквозь противников и блокируются только границами уровня (сторонами прямоугольника, описывающего уровень). На самих противников лучи не влияют.
На уровне, который в разработке у Иры, ровно $$$n$$$ противников. Противник $$$i$$$ находится в точке $$$(x_i, y_i)$$$, и его вероятность стать усиленным равна $$$p_i$$$ (то есть противник усиленный с вероятностью $$$p_i$$$ или базовый с вероятностью $$$1-p_i$$$). Вероятности усиления независимы друг от друга.
Ира хочет оценить ожидаемую сложность уровня. Она решила, что хорошей мерой сложности уровня будет количество частей, на которые уровень делится лазерными лучами. А потому, она хочет подсчитать математическое ожидание количества этих частей.
Помогите ей оценить ожидаемую сложность уровня!
В первой строке заданы три целых числа $$$n$$$, $$$a$$$ и $$$b$$$ ($$$1 \le n \le 100$$$; $$$2 \le a, b \le 100$$$) — количество противников на уровне и размеры данного уровня.
Далее следуют $$$n$$$ строк. В $$$i$$$-й строке заданы три целых числа $$$x_i$$$, $$$y_i$$$ и $$$p'_i$$$ ($$$1 \le x_i \le a - 1$$$; $$$1 \le y_i \le b - 1$$$; $$$1 \le p'_i \le 999999$$$), означающих, что $$$i$$$-й противник расположен в точке $$$(x_i, y_i)$$$ и его вероятность усилиться равна $$$\frac{p'_i}{10^6}$$$.
Никакие два противника не стоят в одной точке.
Выведите одно целое число — математическое ожидание количества частей, на которые лазеры делят уровень, по модулю $$$998244353$$$ (т. е. пусть матожидание количества частей равно $$$\frac{x}{y}$$$ как несократимой дробь; вам нужно вывести $$$x \cdot y^{-1} \bmod 998244353$$$, где $$$y^{-1}$$$ — это такое число, что $$$y \cdot y^{-1} \bmod 998244353 = 1$$$).
1 2 2 1 1 500000
6
2 3 2 1 1 500000 2 1 500000
499122187
Описание первого примера:
С вероятностью $$$\frac{1}{2}$$$, единственный противник останется не усиленным. Тогда уровень будет выглядеть следующим образом ($$$4$$$ части):
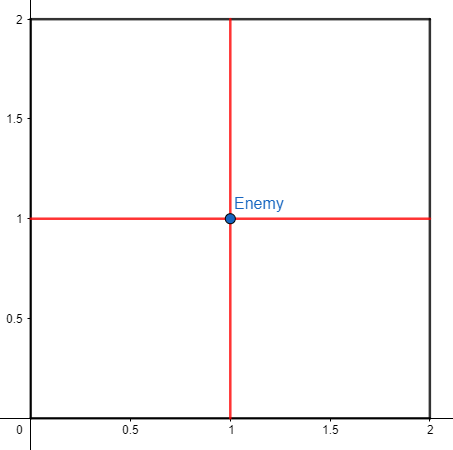
С вероятностью $$$\frac{1}{2}$$$, единственный противник усилится. В таком случае уровень будет выглядеть следующим образом ($$$8$$$ частей):
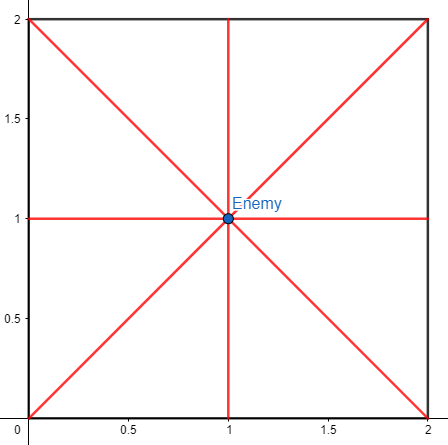
Таким образом, матожидание количества частей равно $$$4 \cdot \frac{1}{2} + 8 \cdot \frac{1}{2} = 6$$$.
| Название |
|---|




