$$$2^k$$$ команд участвуют в плей-офф турнире. Турнир состоит из $$$2^k - 1$$$ игры. Они проводятся следующим образом: во-первых, команды делятся на пары: команда $$$1$$$ играет против команды $$$2$$$, команда $$$3$$$ играет против команды $$$4$$$ (именно в таком порядке) и так далее (таким образом, в этой фазе будет сыграно $$$2^{k-1}$$$ игры). Когда команда проигрывает игру, она выбывает, и каждая игра приводит к выбыванию одной команды (нет ничьих). После этого остается $$$2^{k-1}$$$ команд. Если остается только одна команда, она объявляется чемпионом; в противном случае играется еще $$$2^{k-2}$$$ игр: в первой из них победитель игры «$$$1$$$ против $$$2$$$» играет против победителя игры «$$$3$$$ против $$$4$$$», затем победитель игры «$$$5$$$ против $$$6$$$» играет против победителя игры «$$$7$$$ против $$$8$$$» и так далее. Этот процесс повторяется до тех пор, пока не останется только одна команда.

Место команды в турнире зависит от того, в какой фазе турнира она выбыла:

• команда-победитель турнира занимает место $$$1$$$;
• команда, выбывшая в финале, занимает место $$$2$$$;
• обе команды, выбывшие в полуфинале, занимают место $$$3$$$;
• все команды, выбывшие в четвертьфинале, занимают место $$$5$$$;
• все команды, выбывшие в 1/8 финала, занимают место $$$9$$$, и так далее.

Например, на этой картинке показан возможный ход турнира при $$$k = 3$$$, а также итоговые места команд при таком ходе турнира:

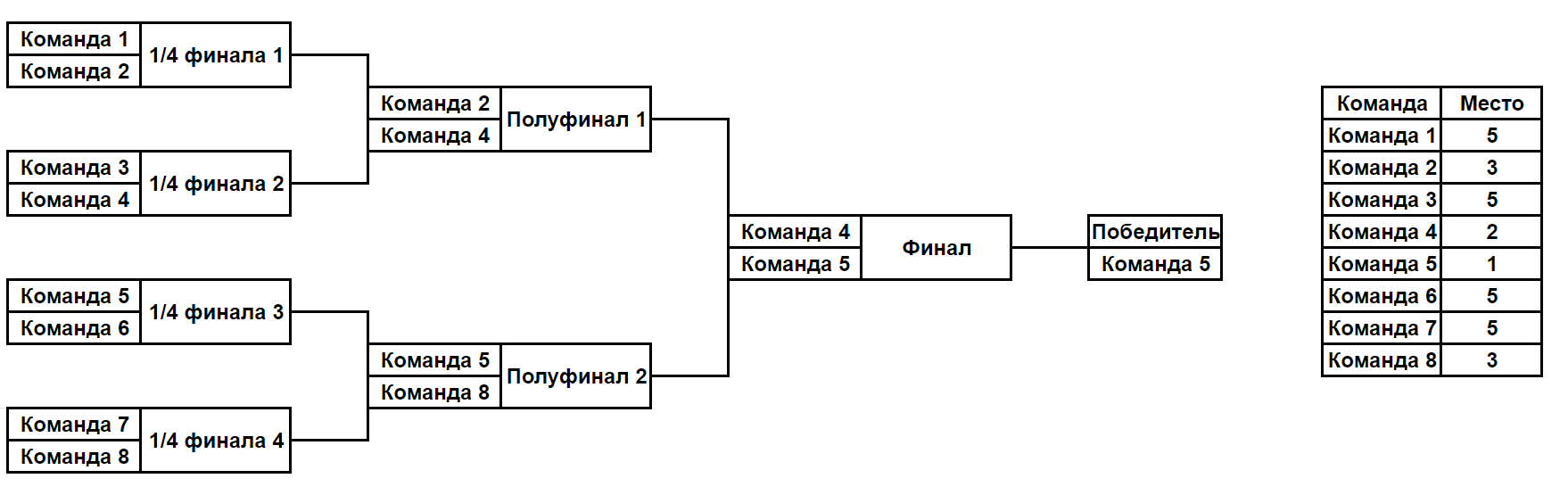
После окончания турнира, который проходил по этим правилам, его результаты были закодированы следующим образом. Пусть $$$p_i$$$ — место, которое заняла $$$i$$$-я команда. Хэш турнира $$$h$$$ считается по формуле $$$h = (\sum \limits_{i=1}^{2^k} i \cdot A^{p_i}) \bmod 998244353$$$, где $$$A$$$ — некоторое заданное целое число.

К сожалению, из-за сбоя системы почти вся информация о прошедшем турнире была утеряна. Остались только значения $$$k$$$, $$$A$$$ и $$$h$$$. Вам нужно по этим трем числам восстановить, какое место заняла какая команда (если это вообще возможно).