| Codeforces Round 742 (Div. 2) |
|---|
| Закончено |
Алиса только недавно изучила сложение. Однако она еще не полностью освоила концепт «переноса»: вместо того, чтобы переносить цифру в следующий разряд, она переносит ее через один разряд.
Например, обычный способ подсчета суммы $$$2039 + 2976$$$ показан ниже:

Однако Алиса подсчитывает сумму следующим образом:
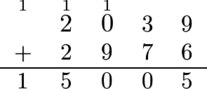
А именно, она делает следующее:
- складывает $$$9$$$ и $$$6$$$, получая $$$15$$$, и переносит $$$1$$$ на два разряда левее, т. е. в столбец «$$$0$$$ $$$9$$$»;
- складывает $$$3$$$ и $$$7$$$, получая $$$10$$$, и переносит $$$1$$$ на два разряда левее, т. е. в столбец «$$$2$$$ $$$2$$$»;
- складывает $$$1$$$, $$$0$$$, и $$$9$$$, получая $$$10$$$, и переносит $$$1$$$ на два разряда левее, т. е. в столбец над знаком плюс;
- складывает $$$1$$$, $$$2$$$ и $$$2$$$, получая $$$5$$$;
- складывает $$$1$$$, получая $$$1$$$.
Алиса пришла к Бобу и рассказала, что она сложила два целых числа и получила в результате $$$n$$$. Но Боб знает, что Алиса сложила числа как умеет. Помогите Бобу посчитать количество упорядоченных пар положительных целых чисел таких, что при сложении методом Алисы получается число $$$n$$$. Обратите внимание, что пары $$$(a, b)$$$ и $$$(b, a)$$$ считаются различными при $$$a \ne b$$$.
Во входных данных находятся несколько наборов входных данных. В первой строке задано одно целое число $$$t$$$ ($$$1 \leq t \leq 1000$$$) — количество наборов входных данных. Далее следуют сами наборы.
В единственно строке каждого набора задано одно целое число $$$n$$$ ($$$2 \leq n \leq 10^9$$$) — число, которое получилось у Алисы.
Для каждого набора входных данных выведите одно целое число — количество упорядоченных пар положительных целых чисел, таких что при сложении своим методом Алиса получит в результате $$$n$$$.
5 100 12 8 2021 10000
9 4 7 44 99
В первом наборе входных данных при сложении Алисой любой из следующих пар: $$$1 + 9$$$, $$$2 + 8$$$, $$$3 + 7$$$, $$$4 + 6$$$, $$$5 + 5$$$, $$$6 + 4$$$, $$$7 + 3$$$, $$$8 + 2$$$ или $$$9 + 1$$$, она получит $$$100$$$ в результате. Изображение, показывающее как Алиса сложит $$$6 + 4$$$, показано ниже:
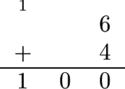
| Название |
|---|




